题目内容
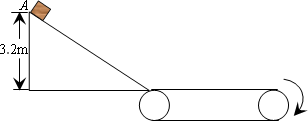
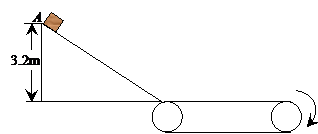
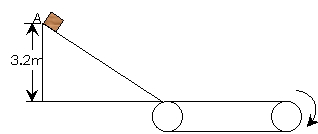
（14分）如图所示，某物块质量为m=1kg，从光滑斜面上的A点由静止自由下滑，A点与斜面底的高度差为h=3.2m。物块经斜面底端冲上传送带的瞬间，无能量损失。传送带长
=9m，与物块间动摩擦因数为μ=0.2。第一次传送带不转动，第二次物块从同一高度滑下，而传送带按照图示方向，以6m/s的速度匀速转动。（g=10m/s2）
（1）物块两次滑过传送带的过程中，摩擦力对物块做功的绝对值之比为多少？
（2）当传送带的转动速度在某一范围内时，物块通过传送带的时间达到最短，求这一最短时间。
解析：（1）根据机械能守恒定律（或动能定理）计算出小物块冲上传送带时的速度：
（1分）
传送带静止时，滑动摩擦力全程都对物块做负功，设摩擦力做功为W1：
= -18J（1分）
又小物块运动到传送带末端时，速度为vt：
（2分）
解得：vt=
m/s ＜6m/s （1分）
所以，当传送带以6m/s速度转动时，物块速度减小到6m/s，就不再减小，此后无摩擦力做功。设此过程摩擦力做功为W2，则：
，末速度v=6m/s（2分）
解得：W2= -14J（1分）
所以，
（1分）
（2）无论传送带转动多快，小物块仅在摩擦力作用下，加速度不会超过：
（1分）
要使时间最短，小物块应该全程加速。当其相对于地的位移等于传送带长时：
（2分）
解得：最短时间t=1s（2分）
练习册系列答案
一线名师提优试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
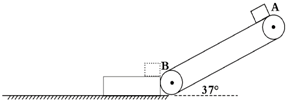如图所示，某传送带与地面倾角θ=37°，AB之间距离
=9m，与物块间动摩擦因数为μ=0.2.第一次传送带不转动，第二次物块从同一高度滑下，而传送带按照图示方向，以6m/s的速度匀速转动.（g=10m/s2）
