题目内容
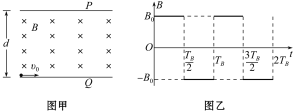
【题目】(2014山东理综，24) 如图甲所示，间距为d、垂直于纸面的两平行板P、Q间存在匀强磁场．取垂直于纸面向里为磁场的正方向，磁感应强度随时间的变化规律如图乙所示．t＝0时刻，一质量为m、带电荷量为＋q的粒子(不计重力)，以初速度v0由Q板左端靠近板面的位置，沿垂直于磁场且平行于板面的方向射入磁场区．当B0和TB取某些特定值时，可使t＝0时刻入射的粒子经Δt时间恰能垂直打在P板上(不考虑粒子反弹)．上述m、q、d、v0为已知量．
(1)若Δt＝
TB，求B0；
(2)若Δt＝
TB，求粒子在磁场中运动时加速度的大小；
(3)若B0＝
，为使粒子仍能垂直打在P板上，求TB.
【答案】 (1) 
(2) 
(3) 
或(
＋arcsin 
)
【解析】 (1)设粒子做圆周运动的半径为R1，由牛顿第二定律得
qv0B0＝
①
据题意由几何关系得
R1＝d②
联立①②式得
B0＝③
(2)设粒子做圆周运动的半径为R2，加速度大小为a，由圆周运动公式得
a＝
④
据题意由几何关系得
3R2＝d⑤
联立④⑤式得
a＝⑥
(3)设粒子做圆周运动的半径为R，周期为T，由圆周运动公式得
T＝
⑦
由牛顿第二定律得
qv0B0＝
⑧
由题意知B0＝
，代入⑧式得
d＝4R⑨
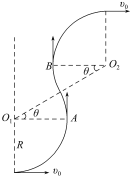
粒子运动轨迹如图所示，O1O2为圆心，O1、O2连线与水平方向的夹角为θ，在每个TB内,只有A、B两个位置才有可能垂直击中P板，且均要求0＜θ＜，由题意可知
T＝
⑩
设经历完整TB的个数为n(n＝0，1，2，3……)
若在A点击中P板，据题意由几何关系得
R＋2(R＋Rsin θ)n＝d
当n＝0时，无解
当n＝1时，联立⑨式得
θ＝
(或sin θ＝
)
联立⑦⑨⑩式得
TB＝
当n≥2时，不满足0＜θ＜90°的要求
若在B点击中P板，据题意由几何关系得
R＋2Rsin θ＋2(R＋Rsinθ)n＝d
当n＝0时，无解
当n＝1时，联立⑨式得
θ＝arcsin 
(或sinθ＝)
联立⑦⑨⑩式得
TB＝(＋arcsin )
当n≥2时，不满足0＜θ＜90°的要求
