Question

根据科普资料介绍，受控核聚变装置中有极高的温度，因而带电粒子将没有通常意义上的”容器”可装，而是借助磁场能约束带电粒子运动这一理论，从而使高速运动的带电粒子束缚在某一磁场区域内，那么，该磁场就成了某种意义上的容器了。
(1)实践表明，如果氦核在磁场区域内沿垂直于磁场方向运动，速度大小V与它在磁场中运动的轨道半径R有关，根据我们已学过的知识，试推导出V与R的关系式。(已知氦核的荷质比为q/m，磁场的磁感强度为B，氦核重力不计)
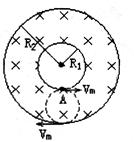
(2)对于上面的”容器”，我们现按下面的简化条件来讨论：如图所示是一个截面为内径R₁，外径R₂的环状区域，区域内有垂直于截面的匀强磁场，已知氦核的荷质比为q/m，磁场的磁感强度为B，若氦核平行于截面从A点以相同速率沿各个方向射入磁场都不能穿出磁场外边界，求氦核的最大速度。

Answer 1

（1）V=qBR/m（2）V_m≤qB(R₂-R₁)/2m

(1).因氦核垂直磁场方向运动且只受洛仑兹力作用,故氦核以速度V在磁感强度为B的匀强磁场中做半径为R的匀速圆周运动,由洛仑兹力和牛顿第二定律得:
qVB=ma=mV²/R       4分  
则V=qBR/m       4分
(2).当氦核以V_m的速度沿与内圆相切时射出,且其轨迹与外圆相切,如图所示,则V_m就是所求的最大速度.设轨迹圆的半径为r,则:
r=(R₂-R₁)/2      3分   
由qVB=mV²/R得:R=mV/qB  
要氦核不穿出磁场边界,则应满足:R≤r  
则V_m≤qBr/m   3分  
即V_m≤qB(R₂-R₁)/2m      3分