题目内容
 (2008?嘉定区二模)如图所示,边长为L的正方形区域abcd内存在着匀强磁场.
(2008?嘉定区二模)如图所示,边长为L的正方形区域abcd内存在着匀强磁场.一个质量为m、电荷量为q、初速度为vo的带电粒子从a点沿ab方向进入磁场,不计重力.若粒子恰好沿BC方向,从c点离开磁场,则磁感应强度B=
| mv0 |
| qL |
| mv0 |
| qL |
| mv02 |
| 2 |
| mv02 |
| 2 |
分析:根据几何关系得出粒子在磁场中做匀速圆周运动的半径,结合半径公式求出磁感应强度的大小.
解答:解:由几何关系得,粒子在磁场中运动的半径r=L.
根据qvB=m
解得B=
.
带电粒子在磁场中运动的速度大小不变,所以动能EK=
mv02.
故答案为:
,
.
根据qvB=m
| v02 |
| L |
解得B=
| mv0 |
| qL |
带电粒子在磁场中运动的速度大小不变,所以动能EK=
| 1 |
| 2 |
故答案为:
| mv0 |
| qL |
| mv02 |
| 2 |
点评:解决本题的关键掌握带电粒子在磁场中做圆周运动的半径公式,结合几何关系求解.

练习册系列答案
相关题目
 (2008?嘉定区二模)一列沿x轴传播的简谐横波某时刻的波形图象如图甲所示.若从此时刻开始计时,则图乙表示a、b、c、d中哪个质点的振动图象( )
(2008?嘉定区二模)一列沿x轴传播的简谐横波某时刻的波形图象如图甲所示.若从此时刻开始计时,则图乙表示a、b、c、d中哪个质点的振动图象( )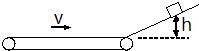 (2008?嘉定区二模)如图所示,小物块从光滑斜面距底边h=0.8m高处由静止下滑,经一与斜面相切的小圆弧滑上足够长的正在匀速运转的水平传送带,传送带的速度为v,方向如图,经过一定时间后,物块从传送带上返回又冲上斜面.当v=3m/s时物块能冲上斜面的高度h1=
(2008?嘉定区二模)如图所示,小物块从光滑斜面距底边h=0.8m高处由静止下滑,经一与斜面相切的小圆弧滑上足够长的正在匀速运转的水平传送带,传送带的速度为v,方向如图,经过一定时间后,物块从传送带上返回又冲上斜面.当v=3m/s时物块能冲上斜面的高度h1= (2008?嘉定区二模)如图所示,某人乘雪橇从雪坡经A点滑至B点,接着沿水平路面滑至C点停止(人与雪橇在B点无能量损失).人与雪橇的总质量为70kg.设雪橇与AB、BC接触面间的动摩擦因数处处相同,忽略空气阻力,表中记录了沿坡滑下过程中的有关数据,请根据图表中的数据解决下列问题:
(2008?嘉定区二模)如图所示,某人乘雪橇从雪坡经A点滑至B点,接着沿水平路面滑至C点停止(人与雪橇在B点无能量损失).人与雪橇的总质量为70kg.设雪橇与AB、BC接触面间的动摩擦因数处处相同,忽略空气阻力,表中记录了沿坡滑下过程中的有关数据,请根据图表中的数据解决下列问题: