题目内容
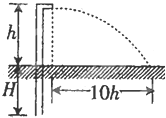 推行节水工程的转动喷水龙头示意图如图所示,龙头距地面高度为h,其喷灌半径可达10h,水泵正常工作时间t内喷出水的质量为m,所用的水是从地下深为H的井中抽取,设水以相同的速率水平喷出,水泵的效率为η,(不计空气阻力,重力加速度为g)求:
推行节水工程的转动喷水龙头示意图如图所示,龙头距地面高度为h,其喷灌半径可达10h,水泵正常工作时间t内喷出水的质量为m,所用的水是从地下深为H的井中抽取,设水以相同的速率水平喷出,水泵的效率为η,(不计空气阻力,重力加速度为g)求:(1)水从喷水龙头喷出的初速度v0
(2)水泵正常工作时间t内对水做的功W
(3)带动水泵的电动机的输出功率P.
分析:(1)水从龙头喷出,做平抛运动,根据平抛运动的知识求出喷水龙头喷出水的初速度;
(2)根据动能定理求解水泵正常工作时间t内对水做的功W;
(3)电动机输出的机械功乘以水泵的效率等于水泵对水所做的功.再由功率公式P=
求出输出功率P.
(2)根据动能定理求解水泵正常工作时间t内对水做的功W;
(3)电动机输出的机械功乘以水泵的效率等于水泵对水所做的功.再由功率公式P=
| W |
| t |
解答:解:(1)水从龙头喷出,做平抛运动,则有:
h=
gt2…①
10h=v0t…②
解得,v0=5
(2)在时间t内,由动能定理得
W-mg(H+h)=
m
解得:W=mg(H+26h)…⑤
(3)依题意可知:带动水泵的电动机的输出功率P=
…⑥
且有:W=ηW总…⑦
解得:P=
…⑧
答:(1)水从喷水龙头喷出的初速度v0是5
;
(2)水泵正常工作时间t内对水做的功W是mg(H+26h);
(3)带动水泵的电动机的输出功率P是
.
h=
| 1 |
| 2 |
10h=v0t…②
解得,v0=5
| 2gh |
(2)在时间t内,由动能定理得
W-mg(H+h)=
| 1 |
| 2 |
| v | 2 0 |
解得:W=mg(H+26h)…⑤
(3)依题意可知:带动水泵的电动机的输出功率P=
| W总 |
| t |
且有:W=ηW总…⑦
解得:P=
| mg(H+26h) |
| ηt |
答:(1)水从喷水龙头喷出的初速度v0是5
| 2gh |
(2)水泵正常工作时间t内对水做的功W是mg(H+26h);
(3)带动水泵的电动机的输出功率P是
| mg(H+26h) |
| ηt |
点评:本题关键要掌握平抛运动的规律,还要熟练运用动能定理和能量守恒定律.

练习册系列答案
相关题目
 如图所示为推行节水工程的转动喷水“龙头”,“龙头”距地面高为h,其喷灌半径可达10h,每分钟喷出水的质量为m,所用的水从地下H深的井里抽取,设水以相同的速率喷出,水泵的效率为?,不计空气阻力(重力加速度为g).则( )
如图所示为推行节水工程的转动喷水“龙头”,“龙头”距地面高为h,其喷灌半径可达10h,每分钟喷出水的质量为m,所用的水从地下H深的井里抽取,设水以相同的速率喷出,水泵的效率为?,不计空气阻力(重力加速度为g).则( )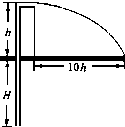 推行节水工程的转动喷水“龙头”如图所示,“龙头”距离地面h,可将水水平喷出,其灌溉半径可达10h,每分钟喷水m,所用的水从地下H深的井里抽取,设水以相同的速率喷出,水泵效率为η,不计空气阻力.试求:
推行节水工程的转动喷水“龙头”如图所示,“龙头”距离地面h,可将水水平喷出,其灌溉半径可达10h,每分钟喷水m,所用的水从地下H深的井里抽取,设水以相同的速率喷出,水泵效率为η,不计空气阻力.试求: 如图所示为推行节水工程的转动喷水“龙头”,水平的喷水“龙头”距地面高为h,其喷灌半径为可达10h,每分钟喷出水的质量为m,所用的水从地下H深的井里抽取,设水以相同的速率喷出,水泵的效率为η,不计空气阻力(重力加速度为g).则( )
如图所示为推行节水工程的转动喷水“龙头”,水平的喷水“龙头”距地面高为h,其喷灌半径为可达10h,每分钟喷出水的质量为m,所用的水从地下H深的井里抽取,设水以相同的速率喷出,水泵的效率为η,不计空气阻力(重力加速度为g).则( )