题目内容
12. 如图所示,光滑水平平台上有一个质量为m的物块,站在水平地面上的人用跨过滑轮的细绳向右拉动物块,细绳不可伸长,不计滑轮的大小、质量和摩擦,在人以速度v从平台边缘正下方匀速向右前进位移s的过程中,始终保持桌面和手的竖直高度差h不变,则在此过程中( )
如图所示,光滑水平平台上有一个质量为m的物块,站在水平地面上的人用跨过滑轮的细绳向右拉动物块,细绳不可伸长,不计滑轮的大小、质量和摩擦,在人以速度v从平台边缘正下方匀速向右前进位移s的过程中,始终保持桌面和手的竖直高度差h不变,则在此过程中( )| A. | 物块做加速运动 | |
| B. | 人对物块做的功为$\frac{1}{2}$mv2 | |
| C. | 人克服物块拉力做的功为$\frac{m{v}^{2}{s}^{2}}{2({h}^{2}+{s}^{2})}$ | |
| D. | 人对物块做功的平均功率为$\frac{m{v}^{3}}{2s}$ |
分析 将人的运动分解为沿绳子方向和垂直于绳子方向,在沿绳子方向上的分速度等于物体的速度,根据平行四边形定则求出物体的速度与人的速度的关系,从而确定物体的运动情况;根据功能关系可求人对物体所做的功;再由功率公式可求得平均功率.
解答 解:A、根据运动的合成与分解,人匀速运动一段位移时,沿绳方向的分速度为vcosθ,cosθ=$\frac{x}{{\sqrt{{h^2}+{x^2}}}}$,所以速率为$\frac{vx}{{\sqrt{{h^2}+{x^2}}}}$,可知物体的速度在增加,故做加速运动;故A正确;
B、当人从平台的边缘处向右匀速前进了s,此时物块的速度大小$v′=vcosθ=v\frac{s}{\sqrt{{h}^{2}+{s}^{2}}}$,根据动能定理得,W=$\frac{1}{2}mv{′}^{2}=\frac{m{v}^{2}{s}^{2}}{2({h}^{2}+{s}^{2})}$.故B错误;C正确
D、人移动的时间t=$\frac{s}{v}$,则重力做功的功率P=$\frac{W}{t}$=$\frac{m{v}^{2}s}{2({h}^{2}+{s}^{2})}$;故D错误;
故选:AC.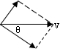
点评 解决本题的关键知道物块的速度等于绳子收缩的速度,等于人运动的沿绳子方向上的分速度,以及能够灵活运用动能定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.一交流电流的图象如图所示,由图可知( )


| A. | 用交流电流表测该电流其示数为10$\sqrt{2}$A | |
| B. | 该交流电流的频率为50Hz | |
| C. | 该交流电流通过10Ω电阻时,电阻消耗的电功率为1000W | |
| D. | 该交流电流瞬时值表达式为i=10$\sqrt{2}$sin628t A |
3. 如图所示,矩形线圈的匝数为N,面积为S,内阻为r,绕OO′轴以角速度ω做匀速转动.当它从如图所示的位置转过90°的过程中,下列说法正确的是( )
如图所示,矩形线圈的匝数为N,面积为S,内阻为r,绕OO′轴以角速度ω做匀速转动.当它从如图所示的位置转过90°的过程中,下列说法正确的是( )
 如图所示,矩形线圈的匝数为N,面积为S,内阻为r,绕OO′轴以角速度ω做匀速转动.当它从如图所示的位置转过90°的过程中,下列说法正确的是( )
如图所示,矩形线圈的匝数为N,面积为S,内阻为r,绕OO′轴以角速度ω做匀速转动.当它从如图所示的位置转过90°的过程中,下列说法正确的是( )| A. | 通过电阻的电荷量为$\frac{NBSπ}{2\sqrt{2}(R+r)}$ | B. | 通过电阻的电荷量为$\frac{NBS}{R+r}$ | ||
| C. | 外力所做的功为$\frac{{N}^{2}{B}^{2}{S}^{2}ω}{2(R+r)}$ | D. | 以上说法都不对 |
20.如图所示,是甲、乙两质点的v-t图象,则由图可知( )


| A. | 0时刻甲的速度大 | B. | 在前5s内甲的速度大 | ||
| C. | 在相等的时间内乙的速度变化大 | D. | 甲、乙两质点都做匀加速直线运动 |
7.在水平平直公路上有A、B两辆汽车,B车在A车前600m处,两车均以v=4m/s匀速直线向前运动.某时刻开始A车开始以a=3m/s2的加速度开始做匀加速直线运动,则A车追上B车需要时间( )
| A. | 10s | B. | 20s | C. | 25s | D. | 30s |
1. 如图所示,质量为m的苹果通过轻绳悬挂在一倾角为θ的光滑斜面上,轻绳与斜面平行,若斜面与苹果处于静止状态,则下列说法不正确的是( )
如图所示,质量为m的苹果通过轻绳悬挂在一倾角为θ的光滑斜面上,轻绳与斜面平行,若斜面与苹果处于静止状态,则下列说法不正确的是( )
 如图所示,质量为m的苹果通过轻绳悬挂在一倾角为θ的光滑斜面上,轻绳与斜面平行,若斜面与苹果处于静止状态,则下列说法不正确的是( )
如图所示,质量为m的苹果通过轻绳悬挂在一倾角为θ的光滑斜面上,轻绳与斜面平行,若斜面与苹果处于静止状态,则下列说法不正确的是( )| A. | 绳对苹果的拉力为mgsinθ | |
| B. | 斜面对苹果的支持力为$\frac{mg}{sinθ}$ | |
| C. | 绳对苹果的拉力与斜面对苹果的支持力合力方向竖直向上 | |
| D. | 绳对苹果的拉力与斜面对苹果的支持力合力大小为mg |
5. 如图,水平放置的密封气缸内的气体被一竖直隔板分隔为左右两部分,隔板可在气缸内无摩擦滑动,右侧气体内有一电热丝.气缸壁和隔板均绝热.初始时隔板静止,左右两边气体温度相等.现给电热丝提供一微弱电流,通电一段时间后切断电源.当缸内气体再次达到平衡时,与初始状态相比( )
如图,水平放置的密封气缸内的气体被一竖直隔板分隔为左右两部分,隔板可在气缸内无摩擦滑动,右侧气体内有一电热丝.气缸壁和隔板均绝热.初始时隔板静止,左右两边气体温度相等.现给电热丝提供一微弱电流,通电一段时间后切断电源.当缸内气体再次达到平衡时,与初始状态相比( )
 如图,水平放置的密封气缸内的气体被一竖直隔板分隔为左右两部分,隔板可在气缸内无摩擦滑动,右侧气体内有一电热丝.气缸壁和隔板均绝热.初始时隔板静止,左右两边气体温度相等.现给电热丝提供一微弱电流,通电一段时间后切断电源.当缸内气体再次达到平衡时,与初始状态相比( )
如图,水平放置的密封气缸内的气体被一竖直隔板分隔为左右两部分,隔板可在气缸内无摩擦滑动,右侧气体内有一电热丝.气缸壁和隔板均绝热.初始时隔板静止,左右两边气体温度相等.现给电热丝提供一微弱电流,通电一段时间后切断电源.当缸内气体再次达到平衡时,与初始状态相比( )| A. | 右边气体温度升高,左边气体温度不变 | |
| B. | 左右两边气体温度都升高 | |
| C. | 左边气体压强增大 | |
| D. | 右边气体内能的增加量等于电热丝放出的热量 | |
| E. | 右边气体分子平均动能的增加量大于左边的增加量 |
 如图所示,在第二象限的正方形区域Ⅰ内存在着垂直纸面向里的匀强磁场;在第四象限区域Ⅱ存在着垂直纸面向外无限大的匀强磁场,两磁场的磁感应强度均为B,方向相反.一质量为m、电量为e电子由P(-d,d)点,沿x轴正方向射入磁场区域Ⅰ.
如图所示,在第二象限的正方形区域Ⅰ内存在着垂直纸面向里的匀强磁场;在第四象限区域Ⅱ存在着垂直纸面向外无限大的匀强磁场,两磁场的磁感应强度均为B,方向相反.一质量为m、电量为e电子由P(-d,d)点,沿x轴正方向射入磁场区域Ⅰ. 如图示,为一学生用万用电表表盘上的电阻档刻度,某同学把选择开关旋到欧姆档“×100”档,调零后测某一电阻时,指针位置如图示,则此时电阻的阻值约为200Ω,为使这个电阻测得更准确些,应将开关旋到×10档,但第二次测量前必须欧姆调零.
如图示,为一学生用万用电表表盘上的电阻档刻度,某同学把选择开关旋到欧姆档“×100”档,调零后测某一电阻时,指针位置如图示,则此时电阻的阻值约为200Ω,为使这个电阻测得更准确些,应将开关旋到×10档,但第二次测量前必须欧姆调零.