题目内容
20.绳系着装水的水桶,在竖直平面内做圆周运动,水的质量m=0.5kg,绳长L=40cm,求:(1)桶的速度为3m/s时,桶在最高点么时水能不能流出?
(2)水对桶底的压力为15N时,桶在最高点速率v2是多大?
分析 (1)水桶运动到最高点时,水不流出恰好不流出时由水受到的重力刚好提供其做圆周运动的向心力,根据牛顿第二定律求解最小速率,进而判断水会不会流出;
(2)以水为研究对象,分析受力情况:重力和桶底的弹力,其合力提供水做圆周运动的向心力,由牛顿第二定律求解速度即可.
解答 解:(1)在最高点水不流出的条件是:重力不大于水做圆周运动所需要的向心力,由牛顿第二定律得:
mg=m$\frac{{{v}_{0}}^{2}}{L}$
解得:${v}_{0}=\sqrt{gL}=2m/s$
因为3m/s>2m/s,所以水不会流出来,
(2)水对桶底的压力为15N时,则桶对水的压力也为15N,对水受力分析,根据向心力公式得:
F+mg=m$\frac{{{v}_{2}}^{2}}{L}$
解得:v2=4m/s
所以桶在最高点的速率v2是4m/s
答:(1)桶的速度为3m/s时,桶在最高点时,水不能流出;
(2)水对桶底的压力为15N时,桶在最高点速率v2是4m/s.
点评 本题应用牛顿第二定律破解水流星节目成功的奥秘,关键在于分析受力情况,确定向心力的来源.

练习册系列答案
相关题目
10.下列说法中正确的是( )
| A. | 力的合成与分解都遵循平行四边形定则 | |
| B. | 一个力只能根据它的实际作用效果进行分解 | |
| C. | 合力的方向一定与最大的分力方向相同 | |
| D. | 一个力只能分解成两个力 |
11.3月30日21时52分,中国在西昌卫星发射中心用长征三号丙运载火箭,成功将首颗新一代北斗导航卫星发射升空,31日凌晨3时34分顺利入倾斜同步轨道(倾斜地球同步轨道平面与赤道平面有一定夹角,其周期与地球自转周期相同).此次反射的亮点在于:首次在运载火箭上增加了一级独立飞行器,实现了卫星直进轨道,在此之前则是通过圆-椭圆-圆的变轨过程实现.则下列说法中正确的是( )
| A. | 倾斜同步轨道半径应小于赤道同步轨道半径 | |
| B. | 一级独立飞行器能大大缩短卫星入轨时间 | |
| C. | 北斗导航卫星的线速度和地球赤道同步卫星的线速度等大 | |
| D. | 倾斜同步轨道卫星经历运行周期的整数倍时间后将到达地球同一地点的上空 |
15.下列关于永动机的说法中错误的是( )
| A. | 第一类永动机违反了能量守恒定律 | |
| B. | 第一类永动机违反了热力学第一定律 | |
| C. | 第二类永动机违反了能量守恒定律 | |
| D. | 第二类永动机违反了热力学第二定律 |
5.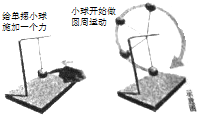 神十航天员王亚平在太空授课时做了图示的实验,用细线悬挂小球,给小球施加一个力后,小球开始在竖直平面内做匀速圆周运动,设神十处于完全失重状态,则小球在运动过程中( )
神十航天员王亚平在太空授课时做了图示的实验,用细线悬挂小球,给小球施加一个力后,小球开始在竖直平面内做匀速圆周运动,设神十处于完全失重状态,则小球在运动过程中( )
 神十航天员王亚平在太空授课时做了图示的实验,用细线悬挂小球,给小球施加一个力后,小球开始在竖直平面内做匀速圆周运动,设神十处于完全失重状态,则小球在运动过程中( )
神十航天员王亚平在太空授课时做了图示的实验,用细线悬挂小球,给小球施加一个力后,小球开始在竖直平面内做匀速圆周运动,设神十处于完全失重状态,则小球在运动过程中( )| A. | 小球所受合力为零 | |
| B. | 重力与细绳的拉力平衡 | |
| C. | 小球只受到细绳的拉力作用 | |
| D. | 细绳的拉力提供了小球作图示运动的向心力 |
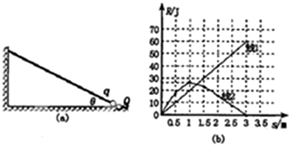 如图(a)所示,倾角θ=30°的光滑固定斜杆底端固定一电量为Q=2×10-4C的正点电荷,将一带正电小球(可视为点电荷)从斜杆的底端(但与Q末接触)静止释放,小球沿斜杆向上滑动过程中能量R随位移S的变化图象如图(b)所示,其中线1为重力势能随位移变化图象,线2为动能随位移变化图象.(g=10m/s2,静电力恒量k=9×109N•m2/C2)
如图(a)所示,倾角θ=30°的光滑固定斜杆底端固定一电量为Q=2×10-4C的正点电荷,将一带正电小球(可视为点电荷)从斜杆的底端(但与Q末接触)静止释放,小球沿斜杆向上滑动过程中能量R随位移S的变化图象如图(b)所示,其中线1为重力势能随位移变化图象,线2为动能随位移变化图象.(g=10m/s2,静电力恒量k=9×109N•m2/C2) (Ⅰ)在“探究平抛运动的运动规律”的实验中,可以描绘出小球平抛运动的轨迹,实验简要步骤如下:
(Ⅰ)在“探究平抛运动的运动规律”的实验中,可以描绘出小球平抛运动的轨迹,实验简要步骤如下: