题目内容
某人在一高楼的楼顶边上做一个竖直下抛实验,他先以10 m/s竖直下抛一个小铁球甲,1秒钟后又以25 m/s竖直下抛另一小铁球乙,如两球同时着地,则抛出点到地面的距离为多少?(g=10 m/s2)
分析:竖直下抛运动是加速度为g的匀加速直线运动,根据匀变速直线运动位移时间公式联立方程即可求解.
解答:解:设甲运动的时间为t,则乙运动的时间为t-1,根据匀变速直线运动位移时间公式得:
v甲t+
g t2=v乙(t-1)+
g (t-1)2
代入数据得:
10t+5t2=25(t-1)+5(t-1)2
解得:t=4s
则抛出点到地面的距离为h=v甲t+
g t2=10×4+
×10×16=120m
答:抛出点到地面的距离为120m
v甲t+
| 1 |
| 2 |
| 1 |
| 2 |
代入数据得:
10t+5t2=25(t-1)+5(t-1)2
解得:t=4s
则抛出点到地面的距离为h=v甲t+
| 1 |
| 2 |
| 1 |
| 2 |
答:抛出点到地面的距离为120m
点评:本题主要考查了匀变速直线运动位移时间公式的直接应用,知道竖直下抛运动是加速度为g的匀加速直线运动,难度不大,属于基础题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 得物体在最后1 s内的位移
得物体在最后1 s内的位移 再根据
再根据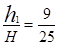 得H="13.9" m,小黄同学的解法是否正确?如果正确,说明理由;如果不正确,请给出正确的解答过程和答案.
得H="13.9" m,小黄同学的解法是否正确?如果正确,说明理由;如果不正确,请给出正确的解答过程和答案. 得物体在最后1 s内的位移
得物体在最后1 s内的位移 再根据
再根据 得H="13.9" m,小黄同学的解法是否正确?如果正确,说明理由;如果不正确,请给出正确的解答过程和答案.
得H="13.9" m,小黄同学的解法是否正确?如果正确,说明理由;如果不正确,请给出正确的解答过程和答案.