题目内容
【题目】如图所示,水平地面上方存在一磁场区域,EF为磁场的上水平边界,在磁场上方有一边长为L的正方形线框ABCD,其质量为m,电阻为R,将线框ABCD从AB边距磁场上边界2L处由静止释放,线框最终落在地面上,线框在整个运动过程中始终处于竖直平面内,且AB边保持水平,以线框AB边进入磁场时刻为计时起点,磁场的磁感应强度B随时间t变化情况如图所示,已知线框进入磁场过程中做匀速运动,磁场区域高度为7L.求: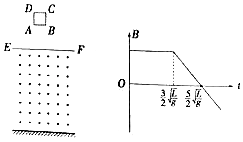
(1)线框AB边刚进入磁场时磁场的磁感应强度
(2)从线框释放到AB边落地过程中,线框中产生的焦耳热.
【答案】
(1)解:设线框AB刚进入磁场时磁场的磁感应强度为B,线框的速度为v,由动能定理可得:2mgL= ![]() mv2
mv2
回路中的电流为:I1= ![]()
线框进入磁场过程中做匀速运动,由平衡条件得:BI1L=mg
联立解得:B= ![]()
答:线框AB边刚进入磁场时磁场的磁感应强度为 ![]() ;
;
(2)解:线框匀速进入磁场的过程中产生的焦耳热:Q1=mgL
设线框进入磁场匀速转动的时间为t0,则t0= ![]() =
= ![]()
线框在磁场中无感应电流的时间为:t1= ![]() ﹣
﹣ ![]() =
= ![]()
磁场变化时,线框中有感应电流,但线框受到的安培力为0,
设线框从完全进入磁场到AB边落地时间为t,有7L﹣L=vt﹣ ![]() gt2
gt2
解得:t=2 ![]()
线框中有感应电流的时间:t2=t﹣t1= ![]()
回路中电流:I2= ![]() =
= ![]()
出磁场产生的焦耳热:Q2=I22Rt22
从线框释放到AB边落地过程中,线框中产生的焦耳热:Q=Q1+Q2= ![]() mgL.
mgL.
答:从线框释放到AB边落地过程中,线框中产生的焦耳热为 ![]() mgL.
mgL.
【解析】本题考查的是电磁感应定律和和力学综合的应用问题,根据安培定律和电磁感应定律,利用受力平衡条件即可计算出匀速运动的速度;综合匀速和匀变速运动规律计算出落地时间;根据功能关系可以计算出产生的焦耳热。