题目内容
 弹簧振子以O点为平衡位置在B、C两点之间做简谐运动,其振动图象如图所示.根据图象求:
弹簧振子以O点为平衡位置在B、C两点之间做简谐运动,其振动图象如图所示.根据图象求:(1)振动的周期;
(2)振子在13s内通过的路程及位移;
(3)求振子运动的位移随时间的变化的关系式;
(4)振子在B点的加速度大小跟2.5s时的加速度大小的比值.
分析:(1)完成一次全振动的时间为一周期,从图上直接读出.
(2)一个周期内质点振动的路程等于4个振幅,关键看13s内经历了几个周期.位移关键看末位置在哪.
(3)简谐运动的表达式为x=Asin(ωt+φ),振幅可从图象上读出,ω=
,φ为初相,等于π.
(4)根据简谐运动的特征a=-
求解加速度大小的比值.
(2)一个周期内质点振动的路程等于4个振幅,关键看13s内经历了几个周期.位移关键看末位置在哪.
(3)简谐运动的表达式为x=Asin(ωt+φ),振幅可从图象上读出,ω=
| 2π |
| T |
(4)根据简谐运动的特征a=-
| kx |
| m |
解答:解:
(1)从振子的振动图象可以看出振动的周期为:T=4s.
(2)从振子的振动图象可以看出振动的振幅为:A=4cm=0.04m,
在13s内通过的路程为:S=
×4A=
×4×4cm=52cm,位移为:x=-4cm.
(3)从振子的振动图象可以看出振动的初相为:φ0=π,
位移随时间变化的关系式为:x=Asin(
t+φ0)=0.04sin(
t+π)m=-0.04sin
tm.
(4)根据x=-0.04sin
t m得知:t=2.5s时,x=-0.04sin(
×2.5)m=0.02
cm.
B的位移大小为 xB=0.04m
根据简谐运动的特征a=-
得知:振子在B点的加速度大小跟2.5s时的加速度大小之比为:aB:a2.5=xB:x2.5=
:1
答:
(1)振动的周期为4s.
(2)振子在13s内通过的路程为52cm,位移为-4cm;
(3)振子运动的位移随时间的变化的关系式为x=-0.04sin
tm.
(4)振子在B点的加速度大小跟2.5s时的加速度大小的比值为
:1.
(1)从振子的振动图象可以看出振动的周期为:T=4s.
(2)从振子的振动图象可以看出振动的振幅为:A=4cm=0.04m,
在13s内通过的路程为:S=
| t |
| T |
| 13 |
| 4 |
(3)从振子的振动图象可以看出振动的初相为:φ0=π,
位移随时间变化的关系式为:x=Asin(
| 2π |
| T |
| π |
| 2 |
| π |
| 2 |
(4)根据x=-0.04sin
| π |
| 2 |
| π |
| 2 |
| 2 |
B的位移大小为 xB=0.04m
根据简谐运动的特征a=-
| kx |
| m |
| 2 |
答:
(1)振动的周期为4s.
(2)振子在13s内通过的路程为52cm,位移为-4cm;
(3)振子运动的位移随时间的变化的关系式为x=-0.04sin
| π |
| 2 |
(4)振子在B点的加速度大小跟2.5s时的加速度大小的比值为
| 2 |
点评:解决本题的关键是能从振动图象上获取信息,会求简谐运动的路程和位移,以及掌握简谐运动的表达式x=Asin(ωt+φ).

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
弹簧振子以O点为平衡位置在B、C两点之间做简谐运动.B、C相距20cm.某时刻振子处于B点.经过0.5s,振子首次到达C点.求:
(1)振动的周期;
(2)振子在5s内通过的路程及偏离平衡位置的位移大小.
(1)振动的周期;
(2)振子在5s内通过的路程及偏离平衡位置的位移大小.
如图1所示,弹簧振子以O点为平衡位置,在A、B两点之间做简谐运动.以向左为正,振子的位移x随时间t的变化如图2所示,则由图可知( )
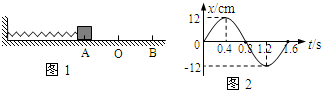
| A、t=0.2s时,振子在O点右侧6cm处 | B、t=1.4s时,振子的速度方向向右 | C、t=0.4s和t=1.2s时,振子的加速度相同 | D、t=0.4s到t=0.8s的时间内,振子的速度逐渐增大 |