题目内容
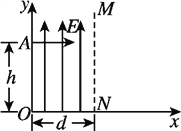
【题目】如图所示，在空间中取直角坐标系xOy，在第一象限内平行于y轴的虚线MN 与y轴距离为d＝8cm，在第一象限内从y轴到MN之间的区域充满一个沿y轴正方向的匀强电场，场强大小为E＝750 V/m.初速度可以忽略的带负电的粒子经过另一个电势差为U＝20V的电场加速后， 从y轴上的A点以平行于x轴的方向射入第一象限区域， OA的距离h＝9cm. 已知带电粒子的比荷为
＝1.6 C/kg，带电粒子的重力忽略不计，求：
(1)粒子进入偏转电场区域的初速度；
(2)试通过计算说明带电粒子从MN边界还是ON边界离开电场；
(3)带电粒子离开偏转电场区域时的速度与进入偏转电场时的速度方向之间的夹角的正切值；
(4)带电粒子经过x轴时离坐标原点O的距离L。
【答案】（1）8m/s（2）从MN离开电场（3）
（4）10cm
【解析】解：（1）粒子在电场中加速由
得
(2)假设粒子从MN离开，则粒子在匀强电场区域的运动时间
因为y＜h，说明以上假设正确，带电粒子从MN离开电场
（3）离开电场时： 
(4)设粒子离开电场后经过时间t′到达x轴，在x轴方向上的位移为x′，则
得 t′＝2.5 ×10-3s
x′＝v0t′ 得 x′＝2 cm
所以 L ＝d ＋x′＝10cm.
综上所述本题答案是：（1）8m/s（2）从MN离开电场（3）
（4）10cm
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
