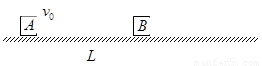
题目内容
质量为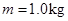 的物块
的物块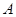 以
以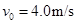 速度沿粗糙水平面滑向静止在水平面上质量为
速度沿粗糙水平面滑向静止在水平面上质量为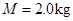 的物块
的物块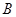 ,物块
,物块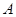 和物块
和物块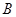 碰撞时间极短,碰后两物块粘在一起。已知物块
碰撞时间极短,碰后两物块粘在一起。已知物块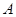 和物块
和物块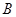 均可视为质点,两物块间的距离为
均可视为质点,两物块间的距离为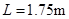 ,两物块与水平面间的动摩擦因数均为
,两物块与水平面间的动摩擦因数均为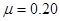 ,重力加速度
,重力加速度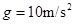 。求:
。求:
(1)物块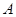 和物块
和物块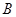 碰撞前的瞬间,物块
碰撞前的瞬间,物块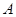 的速度
的速度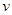 大小;
大小;
(2)物块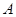 和物块
和物块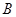 碰撞的过程中,物块
碰撞的过程中,物块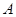 对物块
对物块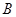 的冲量
的冲量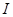 ;
;
(3)物块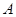 和物块
和物块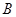 碰撞的过程中,系统损失的机械能
碰撞的过程中,系统损失的机械能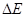 。
。
【答案】
(1)3 m/s (2)2 N·s,水平向右 (3)3 J
【解析】
试题分析:(1)物块 运动到和物块
运动到和物块 碰撞前的瞬间,根据动能定理可知:
碰撞前的瞬间,根据动能定理可知:
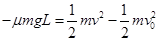 ①
①
解得: 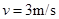
(2)以物块 和物块
和物块 为系统,根据动量守恒可知:
为系统,根据动量守恒可知: ②
②
以物块 为研究对象,根据动量定理可知:
为研究对象,根据动量定理可知: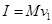 ③
③
解得: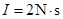 ,方向水平向右
,方向水平向右
(3)以物块A和B为系统,根据能量关系可得: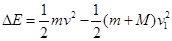 ④
④
解得: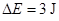
评分标准:①②③④式子各2分,每个结果各1分,方向1分。
考点:本题考查动能定理,动量守恒定律和动量定理等。

练习册系列答案
相关题目
 如图所示,在斜面倾角为θ的斜面底端,垂直斜面有一固定挡板.现有一质量为m(可视为质点)的物块以速度v0从P点沿斜面下滑,已知物块与斜面间动摩擦因数为μ(μ<tanθ),P点距离挡板距离为L,物块与挡板碰撞时无能量损失,不计空气阻力,则有关下列说法正确的是( )
如图所示,在斜面倾角为θ的斜面底端,垂直斜面有一固定挡板.现有一质量为m(可视为质点)的物块以速度v0从P点沿斜面下滑,已知物块与斜面间动摩擦因数为μ(μ<tanθ),P点距离挡板距离为L,物块与挡板碰撞时无能量损失,不计空气阻力,则有关下列说法正确的是( )A、物块第一次与挡板碰撞时的动能为mgLsinθ+
| ||||
| B、第一次与挡板碰后沿斜面上滑的最大距离一定小于L | ||||
| C、从开始到物块静止,物块重力势能的减少量为mgLsinθ | ||||
D、物块在斜面上通过的总路程为
|
如图所示,在斜面倾角为θ的斜面底端,垂直斜面有一固定挡板。现有一质量为m(可视为质点)的物块以速度v0从P点沿斜面下滑,已知物块与斜面间动摩擦因数为μ(μ<tanθ),P点距离挡板距离为L,物块与挡板碰撞时无能量损失,不计空气阻力,则有关下列说法正确的是:
A.物块第一次与挡板碰撞时的动能为 |
| B.第一次与挡板碰后沿斜面上滑的最大距离一定小于L |
C.从开始到物块静止,物块重力势能的减少量为 |
D.物块在斜面上通过的总路程为 |
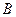 和
和 ,相距
,相距 。物块
。物块 以速度
以速度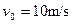 沿水平方向与
沿水平方向与 。已知
。已知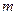 ,
, 倍,物块与地面的动摩擦因数
倍,物块与地面的动摩擦因数 。(设碰撞时间很短,
。(设碰撞时间很短, 取10m/s2)
取10m/s2)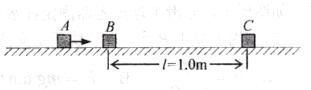
 的速度;
的速度;


