题目内容
【题目】如图所示，宽度为L的光滑平行金属导轨PQ和P′Q′倾斜放置，顶端QQ′之间连接一个阻值为R的电阻和开关S，底端PP′处通过一小段平滑圆弧与一段光滑水平轨道相连．已知水平轨道离地面的高度为h，两倾斜导轨间有一垂直于导轨平面向下的匀强磁场，磁感应强度为B；有两根长均为L、质量均为m、电阻均为R的金属棒AA′、CC′，当金属棒CC′放置在水平轨道右端时，两水平轨道间有竖直方向的磁感应强度为B1的匀强磁场(图中没有画出)，此时开关S处于断开状态；而当金属棒CC′一离开水平轨道，水平轨道间的磁场就马上消失，同时开关S马上闭合．现把金属棒CC′放在水平轨道的右端，金属棒AA′从离水平轨道高为H的地方以较大的初速度v0沿轨道下滑，在极短时间内金属棒CC′就向右离开水平轨道，离开后在空中做平抛运动，落地点到抛出点水平距离为x1，金属棒AA′最后也落在水平地面上，落地点到抛出点的水平距离为x2．不计导轨电阻和空气阻力，忽略金属棒经过PP′处的机械能损失，重力加速度为g，求：
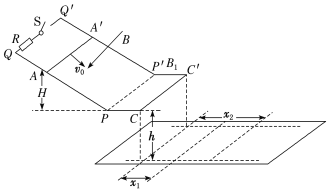
(1)判断B1的方向；
(2)通过CC′的电量q；
(3)整个运动过程中金属棒AA′上产生的焦耳热Q．
【答案】(1)竖直向下(2)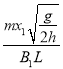
(3)
mgH＋
mv02－
【解析】
(1)金属棒AA′从轨道上向下运动后，由右手定则(或楞次定律)可知电流方向为A→A′，故通过金属棒CC′电流方向为C′→C，由左手定则可知磁场B1的方向为竖直向下．
(2)在金属棒CC′通电的极短时间Δt内，在安培力作用获得向右速度v1,由平抛运动规律得:
h＝gt2
x1＝v1t
由动量定理得
F合Δt＝mΔv
即
B1ILΔt＝mΔv＝mv1－0
解得
q＝IΔt＝
＝
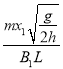
(3)金属棒AA′离开水平轨道后做平抛运动，由平抛运动规律得：
h＝gt2
x2＝v2t
金属棒AA′在轨道上从开始下滑到水平抛出过程中，对整个系统由能量守恒得：
mgH＋mv02＝Q总＋mv12＋mv22
金属棒AA′在轨道上运动时，始终有一个电阻R与金属棒串联，金属棒AA′产生的焦耳热：
Q＝Q总＝mgH＋mv02－
字词句段篇系列答案
