题目内容
某武警总队举行训练表演，一武警战士从距地面高h=34.5m处的一扇窗户外沿一条竖直悬挂的绳子滑下，在下滑的过程中，他先匀加速下滑，此时手脚对悬绳的拉力F1=320N，紧接着再匀减速下滑，此时手脚对悬绳的拉力F2=1040N，滑到地面时速度为安全速度v=3m/s．已知消防队员的质量为m=80kg（g=10m/s2），求他沿绳滑到地面所用的总时间t．
分析：根据牛顿第二定律分别求出战士匀加速和匀减速的加速度，设匀加速的末速度为v′，结合速度位移公式，抓住总位移等于34.5m，求出匀加速运动的末速度，再结合速度时间公式求出匀加速和匀减速运动的时间，从而求出总时间．
解答：解：根据牛顿第二定律得，匀加速运动的加速度：a=
=
m/s2=6m/s2．
匀减速运动的加速度大小：a′=
=
m/s2=3m/s2．
设匀加速运动的末速度为v′，根据速度位移公式得：
+
=h
代入数据解得：v′=12m/s．
则运动的总时间：t=
+
=
+
s=5s．
答：他沿绳滑到地面所用的总时间为5s．
| mg-F1 |
| m |
| 800-320 |
| 80 |
匀减速运动的加速度大小：a′=
| F2-mg |
| m |
| 1040-800 |
| 80 |
设匀加速运动的末速度为v′，根据速度位移公式得：
| v′2 |
| 2a |
| v′2-v2 |
| 2a′ |
代入数据解得：v′=12m/s．
则运动的总时间：t=
| v′ |
| a |
| v′-v |
| a′ |
| 12 |
| 6 |
| 12-3 |
| 3 |
答：他沿绳滑到地面所用的总时间为5s．
点评：本题考查了牛顿第二定律和运动学公式的综合，知道加速度是联系力学和运动学的桥梁．
练习册系列答案
相关题目
某兴趣小组举行遥控赛车比赛，比赛路径如图所示．可视为质点的赛车从起点A出发，沿水平直线轨道运动L=10m后，由B点进入半径R=0.4m的光滑竖直半圆轨道，并通过轨道的最高点C做平抛运动，落地后才算完成比赛．B是半圆轨道的最低点，水平直线轨道和半圆轨道相切于B点．已知赛车质量m=0.5Kg，通电后电动机以额定功率P=3W工作，赛车在水平轨道上受到的阻力恒为f=0.4N，之后在运动中受到的轨道阻力均可不计，g取10m/s2．试求：
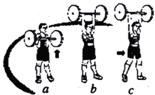如图所示是某运动员在举重训练中的几个分解动作，图中a表示正在上举，b表示上举后停顿片刻，c表示运动员举着杠铃向前水平移动（杠铃高度不变）．关于运动员对杠铃的做功情况，下列说法正确的是（ ）
（2013?海淀区一模）一般来说，正常人从距地面1.5m高处跳下，落地时速度较小，经过腿部的缓冲，这个速度对人是安全的，称为安全着地速度．如果人从高空跳下，必须使用降落伞才能安全着陆，其原因是，张开的降落伞受到空气对伞向上的阻力作用．经过大量实验和理论研究表明，空气对降落伞的阻力f与空气密度ρ、降落伞的迎风面积S、降落伞相对空气速度v、阻力系数c有关（由伞的形状、结构、材料等决定），其表达式是f=