题目内容
15.如图甲所示,质量M=3kg足够长的小车静止在水平面上,半径为R的$\frac{1}{4}$光滑圆轨道的下端与小车的右端平滑对接,质量m=1kg的物块(可视为质点)由轨道顶端静止释放,接着物块离开圆轨道滑上小车.从物块滑上小车开始计时,物块运动的速度随时间变化如图乙所示.己知小车与水平面间的摩擦因数μ0=0.01,重力加速度10m/s2,求: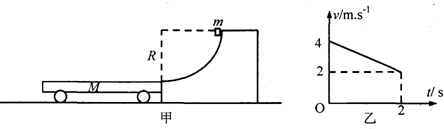
(1)物块经过圆轨道最低点时对轨道的压力F大小;
(2)直到物块与小车相对静止的过程中因摩擦共产生的热量Q.
分析 (1)根据动能定理求出物块到达圆轨道半径,根据牛顿第二定律求出支持力的大小,从而得出对轨道压力F的大小.
(2)根据牛顿第二定律分别求出物块和小车的加速度,当两者速度相等时,保持相对静止,结合运动学公式求出相对静止所需的时间.小车先做匀加速直线运动,当与滑块速度相等后做匀速直线运动,结合运动学公式求出小车运动2s时,小车右端距轨道B端的距离.根据运动学公式求出物块和小车的相对位移,根据Q=f△s求出产生的热量Q.
解答 解:(1)根据机械能守恒定律可得 $mgR=\frac{1}{2}m{v^2}$
解得 R=0.8m
根据牛顿运动定律得物块对轨道的压力大小为 $F-mg=m\frac{v^2}{R}$
解得 F=30N
(2)物块滑上小车后,由图象可知物块的加速度大小为 ${a_1}=1m/{s^2}$
物块与小车间的摩擦力的大小为 f1=ma1=1N
设小车的加速度为a2,则 f1-μ0(M+m)g=Ma2
解得 ${a_2}=0.2m/{s^2}$
当它们达到相同的速度时,有 v=v0-a1tv=a2t
解得 $t=\frac{10}{3}s$
这一过程中,物块的位移为 ${x_1}={v_0}t-\frac{1}{2}{a_1}{t^2}=\frac{70}{9}m$
小车的位移为 ${x_2}=\frac{1}{2}{a_2}{t^2}=\frac{10}{9}m$
物块与小车因摩擦产生的热量为 ${Q_1}={f_1}({x_1}-{x_2})=\frac{20}{3}J$
小车与地面摩擦产生的热量为 ${Q_2}={μ_0}(M+m)g{x_2}=\frac{4}{9}J$
所以共产生的热量为 $Q={Q_1}+{Q_2}=\frac{64}{9}J$
答:
(1)物块经过圆轨道最低点时对轨道的压力F大小是30N;
(2)直到物块与小车相对静止的过程中因摩擦共产生的热量Q是$\frac{64}{9}$J.
点评 此题的关键理清物块和小车的运动规律,运用机械能守恒、功能关系、牛顿第二定律和运动学公式求解.知道摩擦生热与相对路程有关.

| A. | 物体只在重力作用下从静止开始下落的运动,叫做自由落体运动 | |
| B. | 自由落体运动是初速度为零的匀加速直线运动,自由落体运动的加速度叫重力加速度,一般记作g=9.8m/s2 | |
| C. | 因为羽毛下落得比小钢球慢,所以小钢球下落的加速度比羽毛下落的加速度大 | |
| D. | 地球上不同地方的重力加速度的值一般有细微的不同,南北极的重力加速度要比赤道处的重力加速度稍微小一点 |
 如图甲所示,水平面上的不平行导轨MN、PQ上放着两根的光滑导体棒ab、cd,两棒间用绝缘丝线系住;开始时匀强磁场垂直纸面向里,磁感强度B随时间t的变化如图乙所示.则以下说法正确的是( )
如图甲所示,水平面上的不平行导轨MN、PQ上放着两根的光滑导体棒ab、cd,两棒间用绝缘丝线系住;开始时匀强磁场垂直纸面向里,磁感强度B随时间t的变化如图乙所示.则以下说法正确的是( )| A. | 在t0时刻导体棒ab中无感应电流 | |
| B. | 在t0时刻绝缘丝线不受拉力 | |
| C. | 在0~t0时间内导体棒ab始终静止 | |
| D. | 在0~t0时间内回路电流方向是abdca |
| A. | 牛顿首先建立了平均速度、瞬时速度、以及加速度的概念 | |
| B. | 伽利略首先建立了力的概念 | |
| C. | 笛卡尔对牛顿第一定律的建立做出了贡献 | |
| D. | 亚里士多德认为力是维持物体运动的原因 |
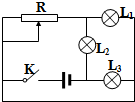 如图所示,电路中电源电动势为ε,内电阻为r,闭合电键K,当滑动变阻器的滑片P从滑线变阻器R的中点位置向左滑动时,小灯泡L1、L2、L3亮度变化情况是( )
如图所示,电路中电源电动势为ε,内电阻为r,闭合电键K,当滑动变阻器的滑片P从滑线变阻器R的中点位置向左滑动时,小灯泡L1、L2、L3亮度变化情况是( )| A. | L1灯变亮,L2灯变暗,L3灯变亮 | B. | L1灯变暗,L2灯变亮,L3灯变暗 | ||
| C. | L1、L2两灯都变亮,L3灯变暗 | D. | L1、L2两灯都变暗,L3灯变亮 |

| A. | 在t=0时刻,质点C沿-x轴方向运动的传播速度为10 m/s | |
| B. | 质点P在t=0.35 s时刻的速度和加速度方向相同 | |
| C. | 质点Q开始振动时运动方向沿y轴正方向 | |
| D. | 在t2=0.9 s时,Q点第一次出现波谷 |
 如图所示,一质量为m、带电荷量为+q的小球,在带有等量异种电荷的两平行金属板间处于匀速运动状态,两平行金属板间的电场强度多大?方向如何?
如图所示,一质量为m、带电荷量为+q的小球,在带有等量异种电荷的两平行金属板间处于匀速运动状态,两平行金属板间的电场强度多大?方向如何?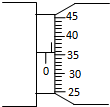 在“测定金属丝的电阻率”的实验中,待测电阻丝阻值约为5Ω
在“测定金属丝的电阻率”的实验中,待测电阻丝阻值约为5Ω