题目内容
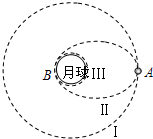 “神州六号”飞船的成功飞行为我国在2010年实现探月计划--“嫦娥工程”获得了宝贵的经验.假设月球半径为R,月球表面的重力加速度为g0,飞船在距月球表面高度为3R的圆形轨道Ⅰ运动,到达轨道的A点点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B再次点火进入月球近月轨道Ⅲ绕月球作圆周运动.求:
“神州六号”飞船的成功飞行为我国在2010年实现探月计划--“嫦娥工程”获得了宝贵的经验.假设月球半径为R,月球表面的重力加速度为g0,飞船在距月球表面高度为3R的圆形轨道Ⅰ运动,到达轨道的A点点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B再次点火进入月球近月轨道Ⅲ绕月球作圆周运动.求:(1)飞船在轨道Ⅰ上的运行速率;
(2)飞船在轨道Ⅲ绕月球运行一周所需的时间.
分析:(1)主要考查圆周运动中向心力公式和万有引力公式的变换,通过联立多项公式获得运行速率和常量的关系;
(2)近月轨道可看做绕转半径为月球半径的圆周,运用圆周运动规律即可解决.
(2)近月轨道可看做绕转半径为月球半径的圆周,运用圆周运动规律即可解决.
解答:解:(1)设月球的质量为M,飞船的质量为m,飞船绕月运动速度为V,飞船绕月运动向心力为F,
则据圆周运动向心力公式得 F=m
①
据万有引力充当向心力得 F=G
②
据月球表面重力充当向心力得 G
=mg0 ③
联立①②③式解得 v=
,
故飞船在轨道Ⅰ上的运行速率为 v=
.
(2)设飞船在轨道Ⅲ绕飞船在轨道月球运行一周所需的时间为T,此时重力充当向心力
则mg0=m(
)2R
∴T=2π
故飞船在轨道Ⅲ绕月球运行一周所需的时间为2π
则据圆周运动向心力公式得 F=m
| V2 |
| (R+3R) |
据万有引力充当向心力得 F=G
| Mm |
| (R+3R)2 |
据月球表面重力充当向心力得 G
| mM |
| R2 |
联立①②③式解得 v=
| 1 |
| 2 |
| g0R |
故飞船在轨道Ⅰ上的运行速率为 v=
| 1 |
| 2 |
| g0R |
(2)设飞船在轨道Ⅲ绕飞船在轨道月球运行一周所需的时间为T,此时重力充当向心力
则mg0=m(
| 2π |
| T |
∴T=2π
|
故飞船在轨道Ⅲ绕月球运行一周所需的时间为2π
|
点评:主要考查圆周运动中各种向心力公式的变换.注意题设条件的完整性.为中档题

练习册系列答案
相关题目