题目内容
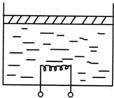如图所示，一圆柱形容器竖直放置，通过活塞封闭着摄氏温度为t的理想气体．活塞的质量为m，横截面积为S，与容器底部相距h．现通过电热丝给气体加热一段时间，结果使活塞又缓慢上升了h，若这段时间内气体吸收的热量为Q，已知大气压强为P0，重力加速度为g，不计器壁向外散失的热量，求：（1）气体的压强；
（2）这段时间内气体的内能增加了多少？
（3）这段时间内气体的温度升高了多少？
分析：（1）以活塞为研究对象，由平衡条件可以求出封闭气体的压强．
（2）由热力学第一定律可以求出气体内能的增加量．
（3）由盖吕萨克定律可以求出气体的末温度，然后求出气体温度的升高量．
（2）由热力学第一定律可以求出气体内能的增加量．
（3）由盖吕萨克定律可以求出气体的末温度，然后求出气体温度的升高量．
解答：解：（1）活塞静止，处于平衡状态，
由平衡条件得：p0S+mg=pS，
解得，封闭气体压强p=p0+
；
（2）气体对外做功为
W=Fh=pSh=(P0+
)Sh=（P0S+mg）h，
由热力学第一定律得：
气体内阻的增量△U=Q-W=Q-（p0S+mg）h；
（3）由盖?吕萨克定律得：
=
=
，
解得：t′=273+2t△t=t′-t=273+t；
答：（1）气体的压强为p0+
；
（2）这段时间内气体的内能增加了=Q-（p0S+mg）h；
（3）这段时间内气体的温度升高了（273+t）K．
由平衡条件得：p0S+mg=pS，
解得，封闭气体压强p=p0+
| mg |
| S |
（2）气体对外做功为
W=Fh=pSh=(P0+
| mg |
| S |
由热力学第一定律得：
气体内阻的增量△U=Q-W=Q-（p0S+mg）h；
（3）由盖?吕萨克定律得：
| V1 |
| T1 |
| V2 |
| T2 |
| hs |
| 273+t |
| 2hs |
| 273+t′ |
解得：t′=273+2t△t=t′-t=273+t；
答：（1）气体的压强为p0+
| mg |
| S |
（2）这段时间内气体的内能增加了=Q-（p0S+mg）h；
（3）这段时间内气体的温度升高了（273+t）K．
点评：知道气体发生的是等压变化，应用平衡条件、热力学第一定律、盖吕萨克定律即可正确解题．
练习册系列答案
名校通行证有效作业系列答案
相关题目
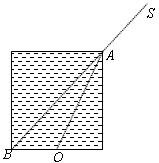
如图所示，一圆柱形容器底面直径和高度相等，当在S处沿容器边缘的A点方向观察空筒时，刚好看到筒底圆周上的B点，保持观察点位置不变，将筒中注满某种液体，可看到筒底的中心点O，试求这种液体的折射率为多少？
随着居民生活水平的提高，纯净水已经进入千家万户．不久前，某省对小城镇市场上的纯净水质量进行了抽测，结果发现九成样品的细菌超标或电导率不合格（电导率是电阻率的倒数，是检验纯净水是否合格的一项重要指标）．
