题目内容
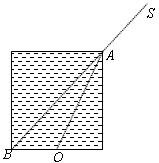
 如图所示,一圆柱形容器底面直径和高度相等,当在S处沿容器边缘的A点方向观察空筒时,刚好看到筒底圆周上的B点,保持观察点位置不变,将筒中注满某种液体,可看到筒底的中心点O,试求这种液体的折射率为多少?
如图所示,一圆柱形容器底面直径和高度相等,当在S处沿容器边缘的A点方向观察空筒时,刚好看到筒底圆周上的B点,保持观察点位置不变,将筒中注满某种液体,可看到筒底的中心点O,试求这种液体的折射率为多少?分析:作出装满液体后的光路图,由几何知识求出入射角与折射角的正弦值,再根据折射定律求出折射率的大小.
解答: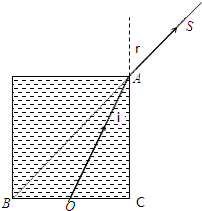 解:作出装满液体后的光路图如图所示.
解:作出装满液体后的光路图如图所示.
设圆柱形容器底面直径和高度均为h.
由几何知识得:
入射角的正弦为:sini=
=
=
折射角的正弦为:sinr=sin45°=
,
所以种液体的折射率为 n=
=
=
答:这种液体的折射率为
.
 解:作出装满液体后的光路图如图所示.
解:作出装满液体后的光路图如图所示.设圆柱形容器底面直径和高度均为h.
由几何知识得:
入射角的正弦为:sini=
| OC | ||
|
| ||||
|
| 1 | ||
|
折射角的正弦为:sinr=sin45°=
| ||
| 2 |
所以种液体的折射率为 n=
| sinr |
| sini |
| ||||
|
| ||
| 2 |
答:这种液体的折射率为
| ||
| 2 |
点评:解决本题的关键正确作出光路图,掌握折射定律,并运用几何知识求解.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
 随着居民生活水平的提高,纯净水已经进入千家万户.不久前,某省对小城镇市场上的纯净水质量进行了抽测,结果发现九成样品的细菌超标或电导率不合格(电导率是电阻率的倒数,是检验纯净水是否合格的一项重要指标).
随着居民生活水平的提高,纯净水已经进入千家万户.不久前,某省对小城镇市场上的纯净水质量进行了抽测,结果发现九成样品的细菌超标或电导率不合格(电导率是电阻率的倒数,是检验纯净水是否合格的一项重要指标).