题目内容
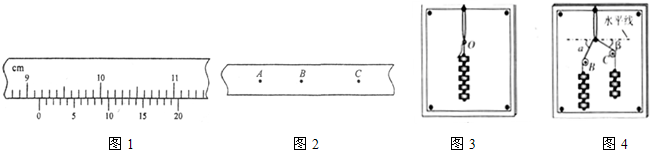
在研究匀变速直线运动的实验中,如图1所示是一次记录小车运动情况的纸带,图中A、B、C、D、E为相邻的计数点,相邻计数点间的时间间隔T=0.10s.
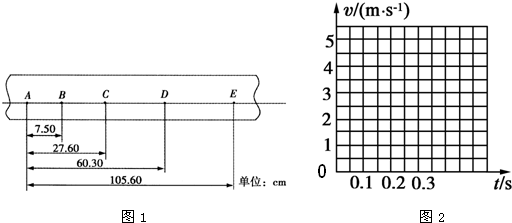
(1)计算各点瞬时速度,vD=
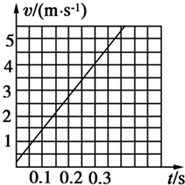
(2)在图2所示的坐标系中作出小车的v-t图线,并根据图线求出a=
(3)将图线延长与纵轴相交,交点的速度是

(1)计算各点瞬时速度,vD=
3.90
3.90
m/s,vC=2.64
2.64
m/s,vB=1.38
1.38
m/s.(2)在图2所示的坐标系中作出小车的v-t图线,并根据图线求出a=
12.8
12.8
m/s2.(3)将图线延长与纵轴相交,交点的速度是
0.15
0.15
m/s,此速度的物理意义是零时刻小车经过A点的速度
零时刻小车经过A点的速度
.分析:(1)根据某段时间内的平均速度等于中间时刻的瞬时速度求出B、C、D的瞬时速度.
(2)作出v-t图线,根据图线的斜率求出加速度的大小.
(3)根据图线得出与纵轴交点的速度.
(2)作出v-t图线,根据图线的斜率求出加速度的大小.
(3)根据图线得出与纵轴交点的速度.
解答:解:(1)D点的瞬时速度vD=
=
m/s=3.90m/s.
C点的瞬时速度vC=
=
m/s=2.64m/s.
B点的瞬时速度vB=
=
m/s=1.38m/s.
(2)根据速度的大小作出v-t图线,图线的斜率等于加速度,所以a=
m/s2=12.8m/s2.
(3)将图线延长与纵轴相交,交点的速度是0.15m/s,意义是零时刻小车经过A点的速度.
故答案为:(1)3.90,2.64,1.38
(2)如图所示,12.8
(3)0.15,零时刻小车经过A点的速度.
| xCE |
| 2T |
| 1.056-0.276 |
| 0.2 |
C点的瞬时速度vC=
| xBD |
| 2T |
| 0.603-0.075 |
| 0.2 |
B点的瞬时速度vB=
| xAC |
| 2T |
| 0.276 |
| 0.2 |
(2)根据速度的大小作出v-t图线,图线的斜率等于加速度,所以a=
| 4.0-0.15 |
| 0.3 |
(3)将图线延长与纵轴相交,交点的速度是0.15m/s,意义是零时刻小车经过A点的速度.
故答案为:(1)3.90,2.64,1.38
(2)如图所示,12.8
(3)0.15,零时刻小车经过A点的速度.

点评:解决本题的关键掌握纸带的处理,会通过纸带求解瞬时速度,以及知道速度时间图线的斜率表示加速度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目