题目内容
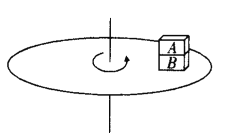
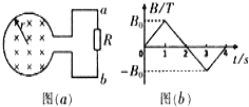
【题目】如图甲所示的装置是由直线加速器改装而成,由N个长度逐个增大的金属圆筒沿水平轴线排列成一串,图中代表性地画了几个圆筒,圆筒的两底面中心开有小孔,一根绝缘光滑细管从中心小孔穿过,各筒相间地连接到频率为f、最大电压值为U0的电源的两端,M、N两点间的电势差UMN随时间变化如图乙所示,现有一电量为+q、质量为m、直径略小于细管内径的小球,沿细管左端射入,并将在圆筒间的缝隙处受到电场力的作用而加速(设圆筒内部没有电场)。缝隙的宽度很小,小球穿过缝隙的时间可以不计。已知t=0时刻小球以v1速度进入第一个圆筒左端,小球多次被加速后通过最右侧圆筒,最后从A点水平向右飞出并以速度v2垂直于偏转电场方向射入一个方向竖直向下、场强为E的匀强电场中,在B点速度方向与电场线成120°角.求:
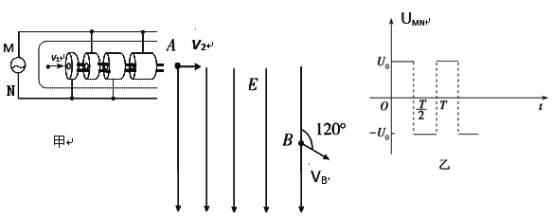
(1)小球从A运动到B的时间tAB;
(2) A、B两点间的电势差UAB;
(3)为使小球从A点射出获得最大能量,各个圆筒的长度应满足什么条件?(用n的形式来表示)
【答案】(1)![]() ;(2)
;(2) ![]() ;(3)
;(3)![]() ,(n=1 ,2.3……)。
,(n=1 ,2.3……)。
【解析】
(1)小球在电场中受电场力和重力作用,根据牛顿第二定律可得
![]()
在B点设小球沿电场方向的速度大小为vy,则有:
![]()
又因为:
![]()
联立解得:![]()
(2)小球竖直位移:
![]()
解得: ![]()
A、B两点间的电势差![]()
解得:![]()
(3)为了使小球获得最大能量,要求小球每次穿过缝隙时,前一个圆筒的电势比后一个的电势高,这就要求小球穿过每个圆筒的时间恰好等于交变电流的半个周期,设第N个圆筒长为Ln,则动能定理得:
![]()
解得:![]()
圆筒的长度
![]()
联立解得:![]() ,(n=1 ,2.3……)
,(n=1 ,2.3……)

练习册系列答案
相关题目