题目内容
19.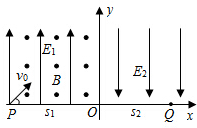 如图所示,竖直平面内的直角坐标系xOy的第Ⅱ象限内有互相垂直的匀强电场和匀强磁场,电场强度E1=2500N/C,方向竖直向上;磁感应强度B=1×103T,方向垂直纸面向外;有一质量m=1×10-2kg、电荷量q=4×10-5C的带正电小球自P点沿水平线成45°角以v0=4m/s的速度射入复合场中,之后小球恰好垂直y轴进入电场强度E2=2500N/C,方向竖直向下的第二个匀强电场中的第Ⅰ象限内,不计空气阻力,g取10m/s2.求:
如图所示,竖直平面内的直角坐标系xOy的第Ⅱ象限内有互相垂直的匀强电场和匀强磁场,电场强度E1=2500N/C,方向竖直向上;磁感应强度B=1×103T,方向垂直纸面向外;有一质量m=1×10-2kg、电荷量q=4×10-5C的带正电小球自P点沿水平线成45°角以v0=4m/s的速度射入复合场中,之后小球恰好垂直y轴进入电场强度E2=2500N/C,方向竖直向下的第二个匀强电场中的第Ⅰ象限内,不计空气阻力,g取10m/s2.求:(1)O点到P点的距离s1;
(2)带电小球经过Q点时与O点的距离s2.
分析 (1)粒子在复合场中电场力和重力平衡,则只在洛仑兹力的作用下做匀速圆周运动,由牛顿第二定律可知粒子的半径,由几何关系可得出两点间的距离;
(2)粒子在电场中,由于重力和电场力的作用做类平抛运动,建立合适的坐标系,则可由运动的合成与分解求得两点间的距离.
解答 解:(1)带电小球在正交的匀强电场和匀强磁场中受到重力G=mg=0.1N; 
电场力F1=Eq=0.1N
即G=F1,故小球在正交的电场由A到C做匀速圆周运动.
根据牛顿第二定律可知Bqv0=m$\frac{{v}_{0}^{2}}{R}$
解得:R=$\frac{m{v}_{0}}{Bq}$=$\frac{1×1{0}^{-2}×4}{1{0}^{3}×4×1{0}^{-5}}$=1m
因小球自P点沿水平线成45°角,由几何关系得:s1=$\frac{\sqrt{2}}{2}$R=$\frac{\sqrt{2}}{2}$m;
(2)带电小球在C点的速度大小仍为v0=4m/s,方向与x轴平行.
由于电场力F2=Eq=0.1N
与重力大小相等,方向相同,
则合力的大小为F=0.2N,方向与初速度垂直,
故小球在第二个电场中作类平抛运动.
建立如图所示的坐标系,沿y方向上,小球的加速度a=$\frac{F}{m}$=$\frac{0.2}{0.01}$=20m/s2;
位移y=$\frac{1}{2}$at2
x方向上有小球的位移x=v0t
由几何关系可知:y=CO=R-AO=(1-$\frac{\sqrt{2}}{2}$)m
解得:t=0.17s
而水平方向,Q到P点的距离为s2=v0t=4×0.17=0.68m,
答:(1)O点到P点的距离$\frac{\sqrt{2}}{2}$m;
(2)带电小球经过Q点时与O点的距离0.68m.
点评 本题考查带电粒子在复合场中的运动,要注意当粒子在复合场中做匀速圆周运动时,粒子受到的电场力与重力平衡,掌握粒子做类平抛运动的处理规律.

| A. | 地球绕太阳公转的周期T地和速度v地 | |
| B. | 太阳质量M日和运行速度v日 | |
| C. | 太阳速度v日和到该天体的距离r | |
| D. | 太阳绕银河系中心运动的速度v日和周期T日 |

| A. | t1时刻小球通过最高点,图乙中S1和S2的面积相等 | |
| B. | t2时刻小球通过最高点,图乙中S1和S2的面积相等 | |
| C. | t1时刻小球通过最高点,图乙中S1和S2的面积不相等 | |
| D. | t2时刻小球通过最高点,图乙中S1和S2的面积不相等 |
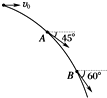 如图所示,一小球以v0=10m/s的速度水平抛出,在落地之前经过空中A、B两点,在A点小球速度方向与水平方向的夹角为45°,在B点小球速度方向与水平方向的夹角为60°(空气阻力忽略不计,g取10m/s2),试求:
如图所示,一小球以v0=10m/s的速度水平抛出,在落地之前经过空中A、B两点,在A点小球速度方向与水平方向的夹角为45°,在B点小球速度方向与水平方向的夹角为60°(空气阻力忽略不计,g取10m/s2),试求: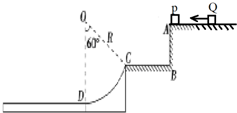 如图所示,有一个可视为质点的P质量为m1=1kg的小物块,从光滑平台上的质量为m2=0.5kg的Q物块以V=3m/s的初速度水平向左撞击P物块后,P物块到达C点时,恰好沿C点的切线方向进入固定在水平地面上的光滑圆弧轨道,已知AB高度差为h=0.6m最后小物块滑上紧靠轨道末端D点的质量为M=3kg的长木板.已知木板上表面与圆弧轨道末端切线相平,木板下表面与水平地面之间光滑,小物块与长木板间的动摩擦因数μ=0.3,圆弧轨道的半径为R=0.4m,C点和圆弧的圆心连线与竖直方向的夹角θ=60°,不计空气阻力,g取10m/s2.求:
如图所示,有一个可视为质点的P质量为m1=1kg的小物块,从光滑平台上的质量为m2=0.5kg的Q物块以V=3m/s的初速度水平向左撞击P物块后,P物块到达C点时,恰好沿C点的切线方向进入固定在水平地面上的光滑圆弧轨道,已知AB高度差为h=0.6m最后小物块滑上紧靠轨道末端D点的质量为M=3kg的长木板.已知木板上表面与圆弧轨道末端切线相平,木板下表面与水平地面之间光滑,小物块与长木板间的动摩擦因数μ=0.3,圆弧轨道的半径为R=0.4m,C点和圆弧的圆心连线与竖直方向的夹角θ=60°,不计空气阻力,g取10m/s2.求: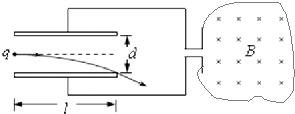 如图所示,一面积为a2导线框内有一匀强磁场,磁场方向垂直于导线框所在平面向内,导线框的左端通过导线接一对水平放置的金属板,两板间的距离为d,板长l=3d.t=0时,磁场的磁感应强度从B0开始均匀增加,同时,在金属板的左侧有一质量为m、电荷量为q的带正电粒子以大小为v0的初速度沿两板间的中线向右射入两板间,恰好从下板的边缘射出,忽略粒子的重力作用.求:
如图所示,一面积为a2导线框内有一匀强磁场,磁场方向垂直于导线框所在平面向内,导线框的左端通过导线接一对水平放置的金属板,两板间的距离为d,板长l=3d.t=0时,磁场的磁感应强度从B0开始均匀增加,同时,在金属板的左侧有一质量为m、电荷量为q的带正电粒子以大小为v0的初速度沿两板间的中线向右射入两板间,恰好从下板的边缘射出,忽略粒子的重力作用.求: