题目内容
4. 在光滑绝缘的水平面上,左侧平行极板间有水平方向的匀强电场,右侧圆筒内有竖直方向的匀强磁场,磁感应强度大小为B,俯视图如图所示,圆心为O,半径为R.一质量为m、电荷量为q的带电小球(可视为质点),初始位置在A点,现由静止经电场加速后从C孔沿直径射入磁场区域,小球和圆筒壁的碰撞没有动能和电荷量损失.B、R、m、q均为已知量,圆筒仅有一个出入口C.
在光滑绝缘的水平面上,左侧平行极板间有水平方向的匀强电场,右侧圆筒内有竖直方向的匀强磁场,磁感应强度大小为B,俯视图如图所示,圆心为O,半径为R.一质量为m、电荷量为q的带电小球(可视为质点),初始位置在A点,现由静止经电场加速后从C孔沿直径射入磁场区域,小球和圆筒壁的碰撞没有动能和电荷量损失.B、R、m、q均为已知量,圆筒仅有一个出入口C.(1)求平行板间电压U和小球在磁场中运动半径r的函数关系式;
(2)小球与圆筒壁碰撞两次后恰好从出入口C返回,求它在磁场中运动的时间;
(3)小球能从出入口C返回且不会跨越C点,平行板间所加电压U应满足什么条件?
分析 (1)对直线加速过程根据动能定理列式得到速度与电压U的关系.在磁场中,由洛伦兹力提供向心力,根据牛顿第二定律列式得到半径与速度的关系,最后联立求解即可;
(2)小球与圆筒壁碰撞两次后恰好从出入口C返回,碰撞点将圆筒三等分,画出轨迹图,由几何关系确定出轨迹对应的圆心角,分析时间与周期的关系进行求解.
(3)小球能从出入口C返回且不会跨越C点,设小球经过n个相同圆弧顺次排列后刚好经过C点离开入口.每段圆弧对应磁场区域圆的圆心角为$\frac{2π}{n}$,由几何关系求出粒子轨道半径表达式,由第1小题r的表达式求解U.
解答 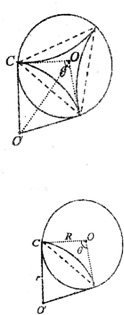 解:(1)设粒子在磁场中圆周运动的线速度大小为v,轨迹半径为r.
解:(1)设粒子在磁场中圆周运动的线速度大小为v,轨迹半径为r.
小球在电场中加速过程,根据动能定理,有:
qU=$\frac{1}{2}m{v}^{2}$;
小球在磁场中运动的过程,根据牛顿第二定律,有:qvB=m$\frac{{v}^{2}}{r}$;
联立解得:U=$\frac{q{B}^{2}{r}^{2}}{2m}$;
(2)小球与圆筒壁碰撞两次后恰好从出入口C返回,轨迹如图所示:
由几何知识得:θ=$\frac{2π}{3}$
则轨迹圆弧对应的圆心角为 $\frac{π}{3}$
小球做圆周运动的周期为 T=$\frac{2πm}{qB}$
则小球在磁场中运动的时间 t=$\frac{3×\frac{π}{3}}{2π}T$=$\frac{πm}{qB}$
(2)据题意可知,设小球经过n个相同圆弧顺次排列后刚好经过C点离开入口.
则每段圆弧对应磁场区域圆的圆心角为 θ=$\frac{2π}{n}$,(n=3,4,5,6…)
小球的轨迹半径:r=Rtan$\frac{θ}{2}$;
由U=$\frac{q{B}^{2}{r}^{2}}{2m}$得 U=$\frac{q{B}^{2}{R}^{2}(tan\frac{π}{n})^{2}}{2m}$,(n=3,4,5,6…).
答:
(1)平行板间电压U和小球在磁场中运动半径r的函数关系式为 U=$\frac{q{B}^{2}{r}^{2}}{2m}$;
(2)小球与圆筒壁碰撞两次后恰好从出入口C返回,它在磁场中运动的时间为 $\frac{πm}{qB}$;
(3)小球能从出入口C返回且不会跨越C点,平行板间所加电压U应满足的条件为:U=$\frac{q{B}^{2}{R}^{2}(tan\frac{π}{n})^{2}}{2m}$,(n=3,4,5,6…).
点评 本题关键明确带电粒子的运动规律,画出运动轨迹,然后根据几何关系求解出半径,再根据动能定理和牛顿第二定律列式求解.在求小球在磁场中运动时间时,要注意公式t=$\frac{α}{2π}$T中α对应的圆心角,不是磁场区域的圆心角.

| A. | 光的干涉说明光是横波 | |
| B. | 自然光在水面反射时,反射光和折射光都是一定程度的偏振光 | |
| C. | 在真空中电磁波的频率越高,传播速度越小 | |
| D. | 在不同惯性系中,光在真空中沿不同方向的传播速度不同 |
 如图所示,在场强大小为 E 的匀强电场中,有一个边长为L的正方形区域,正方形的一条边与电场方向平行.质量为m、电荷量绝对值为q的电子从某一条边的中点,以初速度v0射入该区域.初速度的方向垂直指向对边,但电子没有从对边飞出.下列说法正确的是( )
如图所示,在场强大小为 E 的匀强电场中,有一个边长为L的正方形区域,正方形的一条边与电场方向平行.质量为m、电荷量绝对值为q的电子从某一条边的中点,以初速度v0射入该区域.初速度的方向垂直指向对边,但电子没有从对边飞出.下列说法正确的是( )| A. | 电场方向可能与初速度方向相反 | |
| B. | 电场方向可能与初速度方向垂直 | |
| C. | 电子离开该区域时,动能可能为$\frac{1}{2}$mv02 | |
| D. | 电子离开该区域时,动能可能为$\frac{1}{2}$mv02+$\frac{1}{2}$qEL |
 如图所示,半圆形轨道凹槽静止放置在水平地面上,A点位于半圆形凹槽左边缘,B点位于凹槽上某一点,轨道半径为R,在AB间斜靠一光滑且足够长的木板,在A点有a、b两球(视为质点),a球由静止释放沿斜面下滑到B点,同时b球以某速度v0水平抛出,正好打在B点,则下列说法正确的是( )
如图所示,半圆形轨道凹槽静止放置在水平地面上,A点位于半圆形凹槽左边缘,B点位于凹槽上某一点,轨道半径为R,在AB间斜靠一光滑且足够长的木板,在A点有a、b两球(视为质点),a球由静止释放沿斜面下滑到B点,同时b球以某速度v0水平抛出,正好打在B点,则下列说法正确的是( )| A. | a、b两球有可能同时到达B点 | |
| B. | b球打在B点的速度方向可能垂直于该点的切线方向 | |
| C. | 若a球到达B点的时间是b球的两倍,则木板与水平方向的夹角是60° | |
| D. | 撤去木板,如果v0=$\sqrt{gR}$时,则可判断b球落点位于凹槽最低点的右侧 |
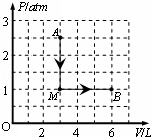 如图所示,一定质量的理想气体,处在A状态时,温度为tA=27℃,则气体从状态A等容变化到状态M,再等压变化到状态B的过程中,对外所做的功W和在状态B的温度tB分别为(取1atm=1.0×105 Pa)( )
如图所示,一定质量的理想气体,处在A状态时,温度为tA=27℃,则气体从状态A等容变化到状态M,再等压变化到状态B的过程中,对外所做的功W和在状态B的温度tB分别为(取1atm=1.0×105 Pa)( )| A. | W=300 J tB=27℃ | B. | W=300 J tB=-33℃ | ||
| C. | W=750 J tB=-33℃ | D. | W=750 J tB=27℃ |
 以不同的抛射角抛出三个小球A、B、C,三球在空中的运动轨迹如图所示,下列说法中正确的是( )
以不同的抛射角抛出三个小球A、B、C,三球在空中的运动轨迹如图所示,下列说法中正确的是( )| A. | A、B、C三球在运动过程中,加速度都相同 | |
| B. | B球的射程最远,所以最迟落地 | |
| C. | A球的射高最大,所以最迟落地 | |
| D. | A、C两球的水平位移相等,所以两球的水平速度分量相等 |
 如图所示,两条平行金属导轨ab、cd置于匀强磁场中,磁场方向垂直金属导轨平面,两导轨间的距离L=0.6m,金属杆MN沿两条导轨向右匀速滑动,速度v0=10m/s,产生的感应电动势为3V,已知金属到杆MN的电阻r=1Ω,外接电阻R=8Ω.求:
如图所示,两条平行金属导轨ab、cd置于匀强磁场中,磁场方向垂直金属导轨平面,两导轨间的距离L=0.6m,金属杆MN沿两条导轨向右匀速滑动,速度v0=10m/s,产生的感应电动势为3V,已知金属到杆MN的电阻r=1Ω,外接电阻R=8Ω.求: ”形状金属杆MNPQGH在辐向磁场中也以角速度ω匀速转动,如图乙所示,图丙为发电机的截面图,已知NP=GQ=R,PQ=L,MH两端接入电阻r,其余电阻不计.
”形状金属杆MNPQGH在辐向磁场中也以角速度ω匀速转动,如图乙所示,图丙为发电机的截面图,已知NP=GQ=R,PQ=L,MH两端接入电阻r,其余电阻不计.