题目内容
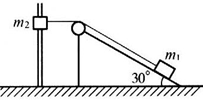如图所示，一轻绳通过无摩擦的定滑轮与放在倾角为30°的光滑斜向上的物体m1连接，另一端和套在光滑竖直杆上的物体m2连接，图中定滑轮到竖直杆的距离为
m，又知当物体m2由图中位置从静止开始下滑1m时，m1和m2受力恰好平衡．
求：
（1）m2下滑过程中的最大速度．
（2）m2下滑的最大距离．
解：（1）以两个物体组成的系统为研究对象，只有重力对系统做功，其机械能守恒，当m1和m2受力恰好平衡时，速度最大，则有
m2gh=m1g（
-r）sin30°+
+
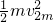
当物体m2由图中位置从静止开始下滑1m时，由几何关系得知，拉m2的绳子与竖直方向的夹角为60°
则v1m=
由平衡条件得：Tcos60°=m2g，T=m1gsin30°，则得，m1=4m2
由题，r=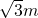
，h=1m，联立解得，vm=2.15m/s
（2）设m2下滑的最大距离为x，此时两个物体的速度均为零，则有
m2gx=m1g（
-r）sin30°
代入解得，x=2.3m
答：（1）m2下滑过程中的最大速度是2.15m/s．
（2）m2下滑的最大距离是2.3m．
分析：（1）以两个物体组成的系统为研究对象，只有重力对系统做功，其机械能守恒．当m1和m2受力恰好平衡时，速度最大，由平衡条件和机械能守恒定律求解最大速度．
（2）当两个物体的速度到达零时，m2下滑的距离最大，再由机械能守恒定律求解最大距离．
点评：本题是绳系的系统机械能守恒问题，平衡只是其中的一个状态，由平衡条件和机械能守恒定律及几何知识结合求解，难度适中．
m2gh=m1g（
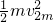
-r）sin30°++当物体m2由图中位置从静止开始下滑1m时，由几何关系得知，拉m2的绳子与竖直方向的夹角为60°
则v1m=
由平衡条件得：Tcos60°=m2g，T=m1gsin30°，则得，m1=4m2
由题，r=
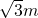，h=1m，联立解得，vm=2.15m/s（2）设m2下滑的最大距离为x，此时两个物体的速度均为零，则有
m2gx=m1g（
-r）sin30°代入解得，x=2.3m
答：（1）m2下滑过程中的最大速度是2.15m/s．
（2）m2下滑的最大距离是2.3m．
分析：（1）以两个物体组成的系统为研究对象，只有重力对系统做功，其机械能守恒．当m1和m2受力恰好平衡时，速度最大，由平衡条件和机械能守恒定律求解最大速度．
（2）当两个物体的速度到达零时，m2下滑的距离最大，再由机械能守恒定律求解最大距离．
点评：本题是绳系的系统机械能守恒问题，平衡只是其中的一个状态，由平衡条件和机械能守恒定律及几何知识结合求解，难度适中．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
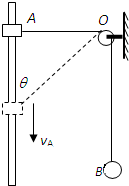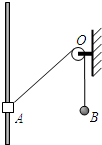如图所示，一轻绳通过无摩擦的小定滑轮O与小球B连接，另一端与套在光滑竖直杆上的小物块A连接，杆两端固定且足够长，物块A由静止从图示位置释放后，先沿杆向上运动．设某时刻物块A运动的速度大小为vA，小球B运动的速度大小为vB，轻绳与杆的夹角为θ．则（ ）
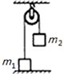（2006?洪泽县模拟）如图所示，一轻绳通过一光滑定滑轮，两端各系一质量分别为m1和m2的物体，m1放在地面上，当m2的质量发生变化时，m1的加速度a的大小与m2的关系大体如图中的（ ）
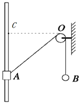（2013?娄底一模）如图所示，一轻绳通过无摩擦的小定滑轮O与小球B连接，另一端与套在光滑竖直杆上的小物块A连接，杆两端固定且足够长，系统从图示位置由静止释放后，A先沿杆向上运动，并能到达与O点等高的C点的上方．设上升过程中某时刻物块A运动的速度大小为vA，小球B运动的速度大小为vB，轻绳与杆的夹角为θ．不计空气阻力，则（ ）
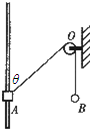如图所示，一轻绳通过无摩擦的小定滑轮O与小球B连接，另一端与套在光滑竖直杆上的小物块A连接，杆两端固定且足够长，物块A由静止从图示位置释放后，先沿杆向上运动．设某时刻物块A运动的速度大小为vA，小球B运动的速度大小为vB，轻绳与杆的夹角为θ．则（ ）
如图所示，一轻绳通过无摩擦的小定滑轮O与小球B连接，另一端与套在光滑竖直杆上的小物块A连接，小球B与物块A质量相等，杆两端固定且足够长．现将物块A由静止从与O等高位置释放后，下落到轻绳与杆的夹角为θ时物块A运动的速度大小为vA，小球B运动的速度大小为vB．则下列说法中正确的是（ ）| A、vA=vB | B、vB=vAsinθ | C、小球B增加的重力势能等于物块A减少重力势能 | D、小球B增加的机械能等于物块A减少机械能 |