题目内容

（2011?丰台区一模）如图所示，长为s的光滑水平面左端为竖直墙壁，右端与半径为R光滑圆弧轨道相切于B点．一质量为m的小球从圆弧轨道上离水平面高为h（h?R）的A点由静止下滑，运动到C点与墙壁发生碰撞，碰撞过程无机械能损失，最终小球又返回A点；之后这一过程循环往复地进行下去，则小球运动的周期为（　　）
分析：h?R，可知小球在光滑圆弧上的运动为单摆运动，根据动能定理求出B点的速度，B到C做匀速直线运动，很容易求出B到C的时间，再根据周期公式求出A到B的时间，即可求出小球的运动周期．
解答：解：根据动能定理mgh=
1
2
mv2-0，v=
2gh
，B到C的时间t1=
s
v
=
s
2gh
，单摆的周期为T=2π
R
g
，所以A到B的时间t2=
π
2
R
g
，所以小球的运动周期为T=2（t1+t2）=π
R
g
+s
2
gh
．故A正确，B、C、D错误．
故选A．
点评：解决本题的关键知道什么样的运动是单摆运动，以及掌握单摆的周期公式T=2π
l
g
．
练习册系列答案
相关题目
（2011?丰台区一模）示波器是一种常见的电学仪器，可以在荧光屏上显示出被检测的电压随时间的变化情况．图甲为示波器的原理结构图，电子经电压Uo加速后进入偏转电场．竖直极板AB间加偏转电压UAB、水平极板间CD加偏转电压UCD，偏转电压随时间变化规律如图乙所示．则荧光屏上所得的波形是（　　）
（2011?丰台区一模）（1）用多用表的欧姆档测量阻值约为几十kΩ的电阻Rx，以下给出的是可能的操作步骤：
a．将两表笔短接，调节欧姆档调零旋钮使指针对准刻度盘上欧姆档的零刻度，断开两表笔．
b．将两表笔分别连接到被测电阻的两端，读出Rx的阻值后，断开两表笔．
c．旋转选择开关，对准欧姆档?1k的位置．
d．旋转选择开关，对准欧姆档?100的位置．
e．旋转选择开关，对准交流“OFF”档，并拔出两表笔．
①请把你认为正确的步骤前的字母按合理的顺序填写在横线上
cabe
cabe
．
②根据如图（1）所示指针位置，此被测电阻的阻值约为
11k
11k
Ω．

（2）某实验小组采用如图（2）所示的装置探究“合外力做功与速度变化的关系”．实验时，先接通电源再松开小车，打点计时器在纸带上打下一系列点．小车所受到的拉力F为0.20N，小车的质量为200g．
①实验前，木板左端被垫起一些，使小车在不受拉力作用时做匀速直线运动．这样做的目的是
AC
AC

A．为了平稳摩擦力
B．增大小车下滑的加速度
C．可使得细绳对小车做的功等于合外力对小车做的功
D．可以用质量较小的砝码就可以拉动小车，以满足砝码质量远小于小车质量的要求
②同学甲选取一条比较理想的纸带做分析．小车刚开始运动时对应在纸带上的点记为起始点O，在点迹清楚段依次选取七个计数点A、B、C、D、E、F、G，相邻计数点间的时间间隔为0.1s．测量起始点O至各计数点的距离，计算计数点对应小车的瞬时速度、计数点与O点之间的速度平方差、起始点O到计算点过程中细绳对小车做的功．其中计数点D的三项数据没有计算，请完成计算并把结果填入表格中．

点迹 O A B C D E F G
x/cm 15.50 21.60 28.61 36.70 45.75 55.75 66.77
v/（m﹒s-1） 0.656 0.755
0.857
0.857
 0.953 1.051
△v 2/（m2﹒s-2） 0.430 0.570
0.734
0.734
 0.908 1.105
W/J 0.0432 0.0572
0.0734
0.0734
 0.0915 0.112
③以W为纵坐标、以△v2为横坐标在方格纸中作出W---△v2图象．B、C、E、F四点已经在图中描出，请在图中描出D点，并根据描点合理画出图象．

④根据图象分析得到的结论
W与△v2成正比
W与△v2成正比
．
⑤同学乙提出利用上述实验装置来验证动能定理．如图所示是打点计时器打出的小车在恒力F作用下做匀加速直线运动的纸带，测量数据已用字母表示在图中．小车质量为m，打点计时器的打点周期为T．利用这些数据可以验证动能定理．

请你判断这种想法是否可行？如果不行，说明理由．如果可行，写出必要的分析与推理．
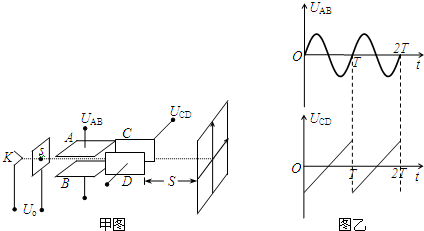
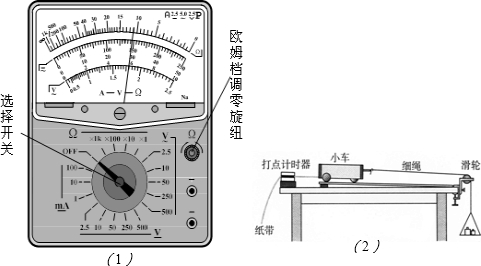
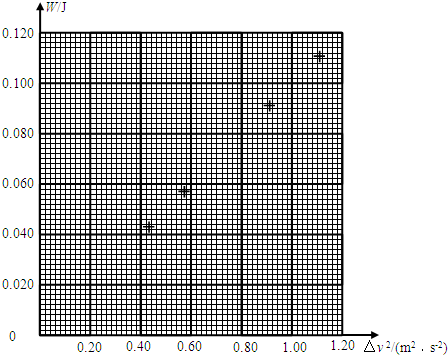
（2011?丰台区一模）如图所示，处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距L=1m．导轨平面与水平面成θ=37°角，下端连接阻值为R的电阻．匀强磁场方向垂直于导轨平面向上，磁感应强度为B=0.4T．质量为0.2kg、电阻不计的金属棒放在两导轨上，棒与导轨垂直且保持良好接触，它们间的动摩擦因数为μ=0.25．金属棒沿导轨由静止开始下滑，当金属棒下滑速度达到稳定时，速度大小为10m/s．（取g=10m/s2，sin 37°=0.6，cos 37°=0.8）．求：
（1）金属棒沿导轨开始下滑时的加速度大小；
（2）当金属棒下滑速度达到稳定时电阻R消耗的功率；
（3）电阻R的阻值．
（2011?丰台区一模）1932年美国物理学家劳伦斯发明了回旋加速器，巧妙地利用带电粒子在磁场中的运动特点，解决了粒子的加速问题．现在回旋加速器被广泛应用于科学研究和医学设备中．

某型号的回旋加速器的工作原理如图甲所示，图为俯视图乙．回旋加速器的核心部分为D形盒，D形盒装在真空容器中，整个装置放在巨大的电磁铁两极之间的强大磁场中，磁场可以认为是匀强在场，且与D形盒盒面垂直．两盒间狭缝很小，带电粒子穿过的时间可以忽略不计．D形盒半径为R，磁场的磁感应强度为B．设质子从粒子源A处时入加速电场的初速度不计．质子质量为m、电荷量为+q．加速器接一定涉率高频交流电源，其电压为U．加速过程中不考虑相对论效应和重力作用．
（1）求质子第1次经过狭缝被加速后进入D形盒运动轨道的半径r1；
（2）求质子从静止开始加速到出口处所需的时间t；
（3）如果使用这台回旋加速器加速α粒子，需要进行怎样的改动？请写出必要的分析及推理．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网