题目内容
某同学在测定匀变速直线运动的加速度时，得到了在不同拉力下的A、B、C、D…等几条较为理想的纸带，并在纸带上每5个点取一个计数点，即相邻两计数点间的时间间隔为0.1s，将每条纸带上的计数点都记为0、1、2、3、4、5…，如图所示甲、乙、丙三段纸带，分别是从三条不同纸带上撕下的．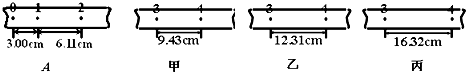
①在甲、乙、丙三段纸带中，属于纸带A的是 ．
②打点记时器打1号计数点时小车的速度为 m/s．（保留两位有效数字）
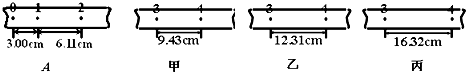
①在甲、乙、丙三段纸带中，属于纸带A的是
②打点记时器打1号计数点时小车的速度为
分析：根据相等时间内的位移之差是一恒量，求出3、4两点的距离，从而确定哪个属于纸带A．根据某段时间内的平均速度等于中间时刻的瞬时速度求出打点计时器打1点的速度．
解答：解：①因为匀变速直线运动中，连续相等时间内的位移之差是一恒量，x12-x01=6.11-3.00cm=3.11cm
则x34-x12=2×3.11=6.22cm，解得x34=6.11+6.22cm=12.33cm，与乙纸带3、4距离接近．故选：乙．
②1点的速度等于0与2之间的平均速度，则v1=
m/s≈0.46m/s．
故答案为：①乙 ②0.46
则x34-x12=2×3.11=6.22cm，解得x34=6.11+6.22cm=12.33cm，与乙纸带3、4距离接近．故选：乙．
②1点的速度等于0与2之间的平均速度，则v1=
| (3.00+6.11)×10-2 |
| 0.2 |
故答案为：①乙 ②0.46
点评：解决本题的关键掌握纸带的处理方法，会通过纸带求解瞬时速度以及加速度，实际上是匀变速直线运动推论的运用．
练习册系列答案
相关题目
（1）要测定个人的反应速度，如图1所示，请你的同学用手指拿着一把长30cm的直尺，他的手抓在28cm处，你的手候在2cm处，当他松开直尺，你见到直尺下落，立即用手抓住直尺，记录抓住处的数据，重复以上步骤多次．现有A、B、C三位同学相互测定反应速度得到的数据（单位：cm，重力加速度g取10m/s2）
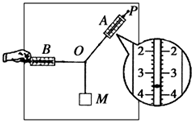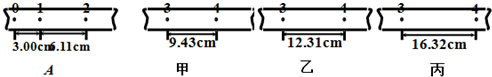
Ⅰ．某同学用如图所示的实验装置来验证
Ⅰ．某同学用如图所示的实验装置来验证
