��Ŀ����
����Ŀ����ͼ����ʾ������ΪM=0.5kg��ľ�徲ֹ�ڹ⻬ˮƽ���ϣ�����Ϊm=1kg������Գ��ٶ�v0=4m/s����ľ�����ˣ������ľ��֮��Ķ�Ħ������Ϊ��=0.2������黬��ľ���ͬʱ����ľ��ʩ��һ��ˮƽ���ҵĺ���F��������Fȡijһֵʱ�������ľ���������ľ�廬����·��Ϊs����ľ��ʩ�Ӳ�ͬ��С�ĺ���F���õ� ![]() �Ĺ�ϵ��ͼ����ʾ������AB�����ƽ�У���AB�ε�������Ϊ1m��1 �� �������Ϊ�ʵ㣬���Ħ�������ڻ���Ħ�������������ٶ�g=10m/s2 ��
�Ĺ�ϵ��ͼ����ʾ������AB�����ƽ�У���AB�ε�������Ϊ1m��1 �� �������Ϊ�ʵ㣬���Ħ�������ڻ���Ħ�������������ٶ�g=10m/s2 �� 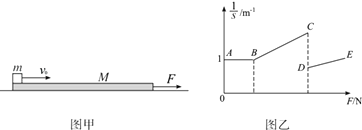
��1��������F=0���������ľ����Ҷ˻��£��������ľ���ϻ��е�ʱ���Ƕ��٣�
��2��ͼ����BCΪֱ�߶Σ���öκ���F��ȡֵ��Χ�� ![]() ������ϵʽ��
������ϵʽ��
���𰸡�
��1��
�⣺�Գ��ٶ�v0Ϊ���������ļ��ٶȴ�С�� ![]()
ľ��ļ��ٶȴ�С�� ![]()
��ͼ��֪���峤L=1m
�������ľ���·�̣� ![]()
������ã� ![]()
��t=1sʱ��������ٶ�Ϊ2m/s��ľ����ٶ�Ϊ4m/s����������ľ���Ҷ˻���ʱ��������ٶȲ�����С��ľ����ٶȣ�t=1sӦ������������ʱ��Ϊ ![]()
��2��
�⣺�ٵ�F��Сʱ����齫��ľ���Ҷ˻��£���F����ijһֵʱ���ǡ�õ���ľ����Ҷˣ������߾��й�ͬ�ٶ�v����ʱt1���� ![]() v=v0��amt1=a1t1
v=v0��amt1=a1t1
λ�ƹ�ϵ��
![]()
������ã� ![]()
��ͼ��֪�����·�̣�s��1m
�����ã�F��1N
�ڵ�F��������ʱ�������١�ľ����٣�������ľ����ijһλ�þ��й�ͬ�ٶȣ������߹��ٺ��ܱ�����Ծ�ֹ����Ħ�������ã�һ������ͬ���ٶ�a���ȼ����˶����� ![]()
f=ma
���ھ�Ħ�����������ֵ�����ԣ�f��fmax=��mg=2N
������ã�F��3N
��������BC�κ���F��ȡֵ��Χ��1N��F��3N��������ϵʽ�� ![]()
����������1�����⣬������F=0���������ľ����Ҷ˻��£��ֱ�������ľ������������������ţ�ٵڶ�����������ٶȣ�Ȼ����λ�ƹ�ϵ�����������2����ͼ��ɿ�����FС��ijһֵF1ʱ��m�����ڰ��ϵ�·��ʼ�յ��ڰ峤S����F����ijһֵF1ʱ���պò���ľ���Ҷ˵��£��˺�һ����Ծ�ֹ�������˶�������ţ�ٵڶ����ɼ��˶�ѧ������ʽ��ץסλ��֮��Ĺ�ϵ��ʽ�������������B��A�����A�����˶���·��S��F��v0�Ĺ�ϵʽ����S=1m���뼴�����F1��
��F1��F��F2ʱ������F������S��С����F=F2ʱ������Sͻ�䣬˵����ʱ��顢ľ���ڴﵽ��ͬ�ٶȺ�ǡ���ٴη�������˶�����齫���ľ����˵��£�
�Զ���ǡ�÷�������˶�ʱ��ľ��ļ��ٶ�Ϊa2 �� ��������ٶ�ҲΪa2 �� ��ţ�ٵڶ�������ʽ������⣻
�����㾫�����������⣬������Ҫ�˽��ȱ���ֱ���˶����ٶȡ�λ�ơ�ʱ��Ĺ�ϵ(�ٶȹ�ʽ��V=V0+at��λ�ƹ�ʽ��s=v0t+1/2at2���ٶ�λ�ƹ�ʽ��vt2-v02=2as�����ϸ�ʽ��Ϊʸ��ʽ��Ӧ��ʱӦ�涨������Ȼ���ʸ����Ϊ��������⣬ͨ��ѡ���ٶȷ���Ϊ�������Ǹ�������һ�µ�ȡ��+��ֵ�����������෴��ȡ��-��ֵ)��

 �����Ļ�������ҵϵ�д�
�����Ļ�������ҵϵ�д�