题目内容
18．
如图所示，物体A和B质量相同，不计大小，用跨过同一高度处的光滑滑轮的细线连接着的．A套在光滑水平杆上，定滑轮离水平杆高度为h=0.2m，开始让连A的细线与水平杆夹角θ=53°，由静止释放，在以后的过程中A所能获得的最大速度为（ ）| A． | 0.5m/s | B． | 1m/s | C． | $\sqrt{2}$m/s | D． | 2m/s |
分析 将A的速度分解为沿绳子方向和垂直于绳子方向，沿绳子方向上的分速度等于B的速度大小，根据该关系得出A、B的速率的关系．当θ=90°时，A的速率最大，此时B的速率为零，根据系统机械能守恒求出A获得的最大速度．
解答 解：将A的速度分解为沿绳子方向和垂直于绳子方向，沿绳子方向上的分速度等于B的速度大小，有：vAcosθ=vB，A、B组成的系统机械能守恒，当θ=90°时，A的速率最大，此时B的速率为零．设AB的质量均为m，根据系统机械能守恒有：
mg（$\frac{h}{sinθ}$-h）=$\frac{1}{2}$m${v}_{A}^{2}$，
代入数据解得：vA=1m/s．选项B正确，ACD错误
故选：B
点评 解决本题的关键知道A沿绳子方向上的分速度等于B的速度大小，以及知道A、B组成的系统机械能守恒，同时要注意对于A和B的运动过程的分析，知道B减少的重力势能转化为A的动能．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
8．关于闭合电路中的感应电动势E、磁通量Φ、磁通量的变化量△Φ以及磁通量的变化率$\frac{△Φ}{△t}$之间的关系，下列说法正确的是（ ）
| A． | Φ=0时，电动势E=0 | B． | $\frac{△Φ}{△t}$=0时，电动势E可能不等于0 | ||
| C． | △Φ很大，电动势E可能很小 | D． | $\frac{△Φ}{△t}$很大，△Φ一定很大 |
9．
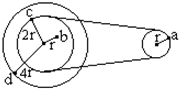如图所示为一皮带传动装置，右轮的半径r，a是它的边缘上的一点，左侧是一轮轴，大轮的半径为4r，小轮的半径为2r．b点在小轮上，到小轮中心的距离为r．c点和d点分别位于小轮和大轮的边缘上．若在传动过程中，皮带不打滑，则（ ）
如图所示为一皮带传动装置，右轮的半径r，a是它的边缘上的一点，左侧是一轮轴，大轮的半径为4r，小轮的半径为2r．b点在小轮上，到小轮中心的距离为r．c点和d点分别位于小轮和大轮的边缘上．若在传动过程中，皮带不打滑，则（ ）| A． | a点与b点的线速度大小相等 | B． | b点与c点的角速度大小相等 | ||
| C． | c点与d点的转速大小相等 | D． | d点与a点的向心加速度大小相等 |
回答下面有关“研究平抛运动”的实验的问题：
13．电磁式打点计时器所接电压是（ ）
| A． | 220V直流电压 | B． | 220V交流电压 | C． | 6V直流电压 | D． | 6V交流电压 |
