题目内容
18.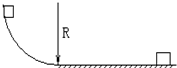 如图所示,一质量m=2kg的物体,从$\frac{1}{4}$粗糙圆弧轨道上端由静止开始下滑到达底端,然后沿水平面向右滑动2m到停止.已知轨道半径R=0.4m,物体与水平面间的动摩擦因数是0.1,重力加速度g=10m/s2.求:
如图所示,一质量m=2kg的物体,从$\frac{1}{4}$粗糙圆弧轨道上端由静止开始下滑到达底端,然后沿水平面向右滑动2m到停止.已知轨道半径R=0.4m,物体与水平面间的动摩擦因数是0.1,重力加速度g=10m/s2.求:(1)物体滑至圆弧轨道底端时的速度大小;
(2)物体滑至圆弧轨道底端时对底端的压力大小;
(3)物体沿圆弧轨道下滑过程中克服摩擦力做功.
分析 (1)对水平面上运动的过程,利用动能定理可以求得物体滑至圆弧轨道底端时的速度大小;
(2)物体做圆周运动,由牛顿第二定律可以求出物体受到的支持力,然后由牛顿第二定律求出物体对轨道的压力.
(3)由动能定理可以求出物体下滑过程中克服摩擦力做的功.
解答 (16分)(1)水平面上:-μmgx=0-$\frac{1}{2}$mv2
物体滑至圆弧轨道底端时的速度大小为:v=2m/s
(2)在圆弧轨道底端有:F-mg=m$\frac{{v}^{2}}{R}$
圆弧轨道对物体的支持力为:F=40N
由牛顿第三定律可知,物体对轨道低端的压力:F′=F=40N;
(3)沿圆弧轨道下滑过程有:mgR-Wf=$\frac{1}{2}$mv2-0,
克服摩擦力做功为:Wf=4J
答:(1)物体滑至圆弧轨道底端时的速度大小2m/s;
(2)物体滑至圆弧轨道底端时对底端的压力大小40N;
(3)物体沿圆弧轨道下滑过程中克服摩擦力做功4J.
点评 分析清楚物体的运动过程及受力情况,由牛顿定律、动能定理即可正确解题,本题难度不大,是一道基础题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
8.甲、乙两车在同一地点同时沿同一方向做直线运动,其v-t图象如图所示,则( )
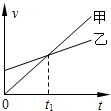

| A. | 它们的初速度均为零 | |
| B. | 甲的加速度大于乙的加速度 | |
| C. | t1时刻,甲的速度大于乙的速度 | |
| D. | 0~t1时间内,甲的位移大于乙的位移 |
9.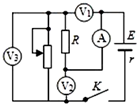 如图所示的电路中,定值电阻R的阻值大于电源内阻r的阻值,将滑动变阻器滑片向下滑动,理想电压表V1、V2、V3示数变化量的绝对值分别为△U1、△U2、△U3,理想电流表A示数变化量的绝对值为△I,则( )
如图所示的电路中,定值电阻R的阻值大于电源内阻r的阻值,将滑动变阻器滑片向下滑动,理想电压表V1、V2、V3示数变化量的绝对值分别为△U1、△U2、△U3,理想电流表A示数变化量的绝对值为△I,则( )
 如图所示的电路中,定值电阻R的阻值大于电源内阻r的阻值,将滑动变阻器滑片向下滑动,理想电压表V1、V2、V3示数变化量的绝对值分别为△U1、△U2、△U3,理想电流表A示数变化量的绝对值为△I,则( )
如图所示的电路中,定值电阻R的阻值大于电源内阻r的阻值,将滑动变阻器滑片向下滑动,理想电压表V1、V2、V3示数变化量的绝对值分别为△U1、△U2、△U3,理想电流表A示数变化量的绝对值为△I,则( )| A. | A的示数增大 | B. | △U1小于△U2 | ||
| C. | △U3与△I的比值等于r | D. | 电阻R消耗的功率一定增大 |
6. 如图所示,质量为m的汽车在平直公路上行驶,所受的阻力恒为车重的k倍.当它以速度v,加速度a加速前进时,发动机的实际功率正好等于额定功率,从该时刻起,发动机始终在额定功率下工作,重力加速度g.则以下分析正确的是( )
如图所示,质量为m的汽车在平直公路上行驶,所受的阻力恒为车重的k倍.当它以速度v,加速度a加速前进时,发动机的实际功率正好等于额定功率,从该时刻起,发动机始终在额定功率下工作,重力加速度g.则以下分析正确的是( )
 如图所示,质量为m的汽车在平直公路上行驶,所受的阻力恒为车重的k倍.当它以速度v,加速度a加速前进时,发动机的实际功率正好等于额定功率,从该时刻起,发动机始终在额定功率下工作,重力加速度g.则以下分析正确的是( )
如图所示,质量为m的汽车在平直公路上行驶,所受的阻力恒为车重的k倍.当它以速度v,加速度a加速前进时,发动机的实际功率正好等于额定功率,从该时刻起,发动机始终在额定功率下工作,重力加速度g.则以下分析正确的是( )| A. | 汽车发动机的额定功率为kmgv | |
| B. | 汽车行驶的最大速度为$\frac{(kg+a)v}{kg}$ | |
| C. | 当汽车加速度减小到$\frac{a}{2}$时,速度增加到2v | |
| D. | 欲使汽车最大速度增加到2倍,则发动机额定功率应增加到4倍 |
13.下列叙述中,符合物理学史实的是( )
| A. | 奥斯特通过实验发现了电磁感应现象 | |
| B. | 法拉第通过实验发现了电流的磁效应 | |
| C. | 牛顿通过理想斜面实验得出了力是维持物体运动状态的原因 | |
| D. | 伽利略研究自由落体运动的思想核心是将实验事实和逻辑推理(包括数学推演)和谐地结合起来 |
3.关于涡流,下列说法中错误的是( )
| A. |  高频冶炼炉是利用涡流来熔化金属的装置 | |
| B. |  家用电磁炉上的锅体中的涡流是由恒定磁场产生的 | |
| C. |  金属探测器靠近金属物体时,金属内会产生涡流 | |
| D. |  变压器的铁芯用相互绝缘的硅钢片叠成能减小涡流 |
10.如图所示,人站在自动扶梯上随扶梯匀速上升,下列说法中正确的是( )
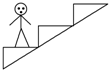

| A. | 人所受的合力方向与自动扶梯运动方向相同 | |
| B. | 人在水平方向将受到向右的摩擦力的作用 | |
| C. | 人只在竖直方向受力作用,且合力为零 | |
| D. | 人在竖直方向所受力的合力不为零 |
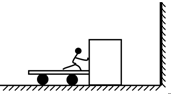 如图所示,小车与木箱紧挨着静止放在光滑的水平冰面上(冰面足够大),现有一男孩站在小车上用力向右迅速推出木箱.推出木箱后人和车的速度大小为4m/s,木箱与竖直墙壁碰撞反弹后恰好不能追上小车.已知人和车的总质量为100kg,木箱的质量为25kg.求:
如图所示,小车与木箱紧挨着静止放在光滑的水平冰面上(冰面足够大),现有一男孩站在小车上用力向右迅速推出木箱.推出木箱后人和车的速度大小为4m/s,木箱与竖直墙壁碰撞反弹后恰好不能追上小车.已知人和车的总质量为100kg,木箱的质量为25kg.求: