题目内容
4．一物体在运动过程中相对于坐标原点的位移与时间关系为x=4t2-6t+8（x、t分别以m、s为单位）则（ ）| A． | 这个物体的初速度为6 m/s | B． | 这个物体的初速度为-6m/s | ||
| C． | 这个物体的加速度为8 m/s2 | D． | 这个物体的加速度为4 m/s2 |
分析 根据匀变速运动的位移随时间变化的关系式即可求解
解答 解：根据匀变速运动的位移随时间变化的关系式x=${v}_{0}t+\frac{1}{2}a{t}^{2}$可知：v0=-6m/s，a=8m/s2
故选：BD
点评 本题考查了匀变速直线运动位移时间公式的直接应用，难度不大，属于基础题
练习册系列答案
相关题目
15．
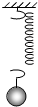如图所示，天花板上悬挂着一劲度系数为k的轻弹簧，弹簧下端拴一个质量为m的小球．小球处于静止状态时（弹簧的形变在弹性限度内），轻弹簧的伸长量等于（ ）
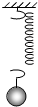如图所示，天花板上悬挂着一劲度系数为k的轻弹簧，弹簧下端拴一个质量为m的小球．小球处于静止状态时（弹簧的形变在弹性限度内），轻弹簧的伸长量等于（ ）| A． | mg | B． | kmg | C． | $\frac{mg}{k}$ | D． | $\frac{k}{mg}$ |
如图所示，在正的点电荷Q的电场中有a、b两点，它们到点电荷Q的距离r1＜r2，a、b两点间的电势差为100V．求
19．
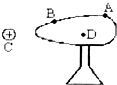如图所示，将原来不带电的绝缘导体AB，置于带正电的点电荷C所形成的电场中，规定大地或无穷远处的电势为零，则有（ ）
如图所示，将原来不带电的绝缘导体AB，置于带正电的点电荷C所形成的电场中，规定大地或无穷远处的电势为零，则有（ ）| A． | 绝缘导体上A、B两点的电势相等，且都为负值 | |
| B． | 绝缘导体上A点的电势高于B点的电势，且都为正值 | |
| C． | 绝缘导体上的感应电荷在导体内部一点D产生的场强大小等于点电荷C在D点产生场强的大小 | |
| D． | 如果用手指瞬间接触导体AB后再把C移走，则导体AB带上正电荷 |
9．
如图所示，倾角为θ=30°的斜面体放在水平地面上，-个重为G的球在水平力F的作用下静止于光滑斜面上，此时水平力的大小为F；若将力F从水平方向逆时针转过某-角度α后，仍保持F的大小不变，且小球和斜面依然保持静止，此时水平地面对斜面体的摩擦力为f，那么F和f的大小分别是（ ）
如图所示，倾角为θ=30°的斜面体放在水平地面上，-个重为G的球在水平力F的作用下静止于光滑斜面上，此时水平力的大小为F；若将力F从水平方向逆时针转过某-角度α后，仍保持F的大小不变，且小球和斜面依然保持静止，此时水平地面对斜面体的摩擦力为f，那么F和f的大小分别是（ ）| A． | F=$\frac{\sqrt{3}}{6}$G，f=$\frac{\sqrt{3}}{3}$G | B． | F=$\frac{\sqrt{3}}{2}$G，f=$\frac{\sqrt{3}}{4}$G | C． | F=$\frac{\sqrt{3}}{3}$G，f=$\frac{\sqrt{3}}{4}$G | D． | F=$\frac{\sqrt{3}}{3}$G，f=$\frac{\sqrt{3}}{6}$g |
16．
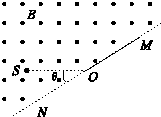如图所示，S处有一电子源，可向纸面内任意方向发射电子，平板MO垂直于纸面，在纸面内的长度L=4.55cm，O与S间的距离d=4.55cm，MO的延长线ON与SO直线的夹角为θ，板所在平面有电子源的一侧区域有方向垂直于纸面向外的匀强磁场，磁感应强度B=2.0×10-4T，电子质量m=9.1×10-31kg，电量e=-1.6×10-19C，不计电子重力．电子源发射速度v=1.6×106m/s的一个电子，该电子打在板上可能位置的区域的长度为l，则（ ）
如图所示，S处有一电子源，可向纸面内任意方向发射电子，平板MO垂直于纸面，在纸面内的长度L=4.55cm，O与S间的距离d=4.55cm，MO的延长线ON与SO直线的夹角为θ，板所在平面有电子源的一侧区域有方向垂直于纸面向外的匀强磁场，磁感应强度B=2.0×10-4T，电子质量m=9.1×10-31kg，电量e=-1.6×10-19C，不计电子重力．电子源发射速度v=1.6×106m/s的一个电子，该电子打在板上可能位置的区域的长度为l，则（ ）| A． | θ=90°时，l=4.55cm | B． | θ=60°时，l=2.275（$\sqrt{4\sqrt{3}-3}$-1cm | ||
| C． | θ=45°时，l=9.1cm | D． | θ=30°时，l=4.55cm |
实验课上老师布置两项任务，①测量一个电流计的内电阻，②测量干电池的电动势和内阻，实验台上准备了如下器材：