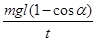题目内容
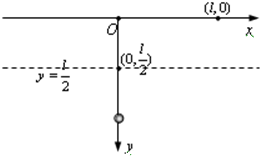 质量为m的小球悬挂于O点,悬线长为l,如图建立平面直角坐标系xOy,y轴沿悬线竖直向下.现将小球拉到(l,0)点后无初速释放,不计空气阻力和钉子的直径,试计算:
质量为m的小球悬挂于O点,悬线长为l,如图建立平面直角坐标系xOy,y轴沿悬线竖直向下.现将小球拉到(l,0)点后无初速释放,不计空气阻力和钉子的直径,试计算:(1)如果在(0,l)点钉一枚钉子可以挡住细线,那么细线刚碰到钉子后对小球的拉力是多大?
(2)如果将钉子钉在y=
| l | 2 |
分析:(1)根据机械能守恒定律求解出最低点速度,然后根据牛顿第二定律列式求解;
(2)碰钉子后的圆周运动的半径越小越容易满足条件;根据机械能守恒定律和牛顿第二定律分别列式后联立求解出临界半径.
(2)碰钉子后的圆周运动的半径越小越容易满足条件;根据机械能守恒定律和牛顿第二定律分别列式后联立求解出临界半径.
解答:解:(1)设小球摆到竖直位置时速度大小为v.
由机械能守恒得:mgl=
mv2;
与钉子碰后:F-mg=m
;
解得:F=5mg;
(2)设小球恰能通过最高点时绕钉子转动的半径为r′,在最高点的速度大小为v′
则在最高点,有mg=m
由机械能守恒:mg(
l-r′)=
mv′2
联立解得:r′=
l
设钉子横坐标x1,根据几何关系,有:
+(
)2=(l-r′)2,
解得x1=±
l
由于钉子必定在以O圆心半径为l的圆内,设直线y=
l与该圆的交战横坐标为x2,则有
+(
l)2=l2
解得x2=±
l
所以要使小球够绕钉子做圆周运动通过最高点,钉子在直线y=
的横坐标范围为:-
l<x≤-
l或
l≤x<
l
答:(1)当钉子在(0,
)点时,细线刚碰到钉子时的拉力为5mg;
(2)钉子所钉的位置的横坐标x的范围为:-
l<x≤-
l或
l≤x<
l.
由机械能守恒得:mgl=
| 1 |
| 2 |
与钉子碰后:F-mg=m
| v2 | ||
|
解得:F=5mg;
(2)设小球恰能通过最高点时绕钉子转动的半径为r′,在最高点的速度大小为v′
则在最高点,有mg=m
| v′2 |
| r′ |
由机械能守恒:mg(
| 1 |
| 2 |
| 1 |
| 2 |
联立解得:r′=
| 1 |
| 3 |
设钉子横坐标x1,根据几何关系,有:
| x | 2 1 |
| l |
| 2 |
解得x1=±
| ||
| 6 |
由于钉子必定在以O圆心半径为l的圆内,设直线y=
| 1 |
| 2 |
| x | 2 2 |
| 1 |
| 2 |
解得x2=±
| ||
| 2 |
所以要使小球够绕钉子做圆周运动通过最高点,钉子在直线y=
| l |
| 2 |
| ||
| 2 |
| ||
| 6 |
| ||
| 6 |
| ||
| 2 |
答:(1)当钉子在(0,
| l |
| 2 |
(2)钉子所钉的位置的横坐标x的范围为:-
| ||
| 2 |
| ||
| 6 |
| ||
| 6 |
| ||
| 2 |
点评:本题关键找出临界过程,然后根据机械能守恒定律和牛顿第二定律列式后联立求解,不难.

练习册系列答案
相关题目
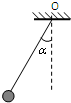 用长为l、不可伸长的细线把质量为m的小球悬挂于O点,将小球拉至悬线偏离竖直方向α角后放手,运动t时间后停在最低点.则在时间t内( )
用长为l、不可伸长的细线把质量为m的小球悬挂于O点,将小球拉至悬线偏离竖直方向α角后放手,运动t时间后停在最低点.则在时间t内( )| A、小球重力做功为mgl(1-cosα) | ||
| B、空气阻力做功为-mglcosα | ||
| C、小球所受合力做功为mglsinα | ||
D、绳拉力做功的功率为
|
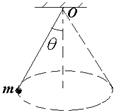 用长为L的轻绳拴住质量为m的小球悬挂于O点,如图,给小球一适当的初速度,使之在水平面内做圆周运动,保持绳与竖直方向的夹角为θ,下列结论正确的是( )
用长为L的轻绳拴住质量为m的小球悬挂于O点,如图,给小球一适当的初速度,使之在水平面内做圆周运动,保持绳与竖直方向的夹角为θ,下列结论正确的是( )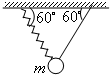 如图所示,用一根轻弹簧和一根轻线将一质量为m的小球悬挂于天花板上,平衡时轻弹簧的中心轴线、轻线与天花板的夹角为60°.则下列说法正确的是( )
如图所示,用一根轻弹簧和一根轻线将一质量为m的小球悬挂于天花板上,平衡时轻弹簧的中心轴线、轻线与天花板的夹角为60°.则下列说法正确的是( )