题目内容
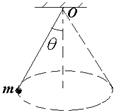用长为L的轻绳拴住质量为m的小球悬挂于O点，如图，给小球一适当的初速度，使之在水平面内做圆周运动，保持绳与竖直方向的夹角为θ，下列结论正确的是（ ）分析：小球在水平面内做匀速圆周运动，靠合力提供向心力，结合牛顿第二定律求出小球的向心加速度和周期的大小．
解答：解：A、小球受重力和拉力两个力作用，靠合力提供向心力，合力的方向指向圆心．故A、B错误．
B、根据牛顿第二定律得，向心力大小为：Fn=mgtanθ，小球做圆周运动的半径为：R=Lsinθ，则由牛顿第二定律得：mgtanθ=ma=mR
，解得a=gtanθ，T=2π
．故C正确，D错误．
故选C．
B、根据牛顿第二定律得，向心力大小为：Fn=mgtanθ，小球做圆周运动的半径为：R=Lsinθ，则由牛顿第二定律得：mgtanθ=ma=mR
| 4π2 |
| T2 |
|
故选C．
点评：解决本题的关键知道小球向心力的来源，结合牛顿第二定律进行求解．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
，径约为地球半径的
.一宇航员在月球上用一根长为l的轻质细绳一端拴住一个质疑为m的小球，另一端固定于空间一点，细绳自由下垂后，他给小球一个水平方向的冲量I0，使小球获得一水平初速度后，在竖直平面内运动，要使小球在向上摆动的过程中，细绳松弛，则宇航员所给小球的水平冲量I0的范围为多大(设地球表面的重力加速度为g)？