��Ŀ����
����Ŀ����ͼ��ʾ��MNPΪ��ֱ����һ�̶�������� ![]() Բ����MN��ˮƽ��NP������NP�˹̶�һ��ֱ���壬NP����Ϊ2m��Բ���뾶Ϊ1m��һ������Ϊ�ʵ�������M�˴Ӿ�ֹ��ʼ�ع���»����뵲�巢����ײ����е�ܲ���ʧ��������ֹͣ��ˮƽ�����ij������֪�����MN�ε�Ħ���ɺ��Բ��ƣ���NP�ι����Ļ���Ħ������Ϊ0.2������飨������
Բ����MN��ˮƽ��NP������NP�˹̶�һ��ֱ���壬NP����Ϊ2m��Բ���뾶Ϊ1m��һ������Ϊ�ʵ�������M�˴Ӿ�ֹ��ʼ�ع���»����뵲�巢����ײ����е�ܲ���ʧ��������ֹͣ��ˮƽ�����ij������֪�����MN�ε�Ħ���ɺ��Բ��ƣ���NP�ι����Ļ���Ħ������Ϊ0.2������飨������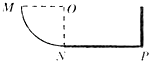
A.�˶��������뵲�巢��1����ײ
B.����Բ�����������{��Ϊ0.6m
C.��NP������һ�ο˷�Ħ��������8J
D.��һ��ڶ��ξ���Բ�����N��ʱ�Թ����ѹ��֮��Ϊ15��7
���𰸡�A,D
���������⣺A����ȫ�������ö��ܶ����ã�mgR����mgs=0��
��ã�s= ![]() ��
��
��NP=2m����֪�˶�����������뵲��ֻ����1����ײ��A�������⣮
B����һ�η���ʱ�������ĸ߶�����ݶ��ܶ����ã�
mgR��mgh����mg2sNP=0��
�������ݵã�h=0.2m��B���������⣮
C����NP������һ�ο˷�Ħ��������Ϊ��
Wf=��mg2sNP=0.8mg��
������������δ֪�����������NP������һ�ο˷�Ħ�������Ĺ���C���������⣮
D����һ�ξ���N��ʱ�����ݶ��ܶ����ã�
mgR= ![]() ��
�� ![]() ��
��
�������ݽ�ã�FN1=3mg��
�ڶ��ξ���N��ʱ�����ݶ��ܶ����ã�
![]() .
. ![]() ��
��
�������ݵã�FN2=1.4mg��
�����У� ![]() ��D�������⣮
��D�������⣮
�ʴ�Ϊ��AD��
������������ʽ�Ͷ��ܶ�����ʽ��⣬��һ�η���ʱ�������ĸ߶����������������δ֪�����������NP������һ�ο˷�Ħ�������Ĺ���