题目内容
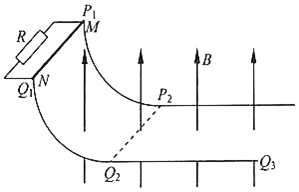
【题目】如图所示，半径为r的
圆弧金属导轨P1P2和Q1Q2位于竖直平面内，它们分别与位于水平面内的金属导轨P2P3和Q2Q3相切于P2、Q2两点，导轨P1P2P3和Q1Q2Q3间距为L，上端P1、Q1用阻值为R的电阻连接，整个装置固定，导轨所在空间存在方向竖直向上、磁感应强度大小为B的匀强磁场。一质量为m的金属杆MN从导轨上端P1Q1处由静止释放，滑至圆弧导轨最低端P2Q2处的速度为v0，然后在水平导轨上运动直至停止。运动过程中杆MN始终垂直于导轨并与导轨保持良好接触，不计导轨和杆MN的电阻，不计一切摩擦。
（1）求杆MN从开始运动到停止的过程中，电阻R上产生的焦耳热；
（2）求杆MN从开始运动到停止的过程中，通过电阻R上的电荷量；
（3）设杆MN停止的位置到P2Q2的距离为s（未知），求杆MN运动到距P2Q2的距离为ns（0＜n＜1）时，电阻R上的热功率。
【答案】（1）mgr（2）
（3）
【解析】
（1）杆MN从开始运动到停止的过程中，根据功能关系可得电阻R上产生的焦耳热为：
Q＝mgr
（2）金属杆滑至圆弧导轨最低端P2Q2处过程中通过R的电荷量为q1，则：
q1＝
水平轨道上运动过程中，根据动量定理可得：
﹣BILt2＝0﹣mv0
此过程中通过R的电荷量为：q2＝It2，
解得：
q2＝
故通过电阻R上的电荷量为：
q＝q1+q2＝
（3）逆向思维，假设杆从距离P2Q2距离为s处开始反向加速到距离P2Q2距离为ns处时的速度为v，则反向加速距离为：
x＝（1﹣n）s
根据动量定理可得：
BILt＝mv
即
＝mv，而
t＝x＝（1﹣n）s
解得：
v＝
根据功率的计算公式可得，杆MN运动到距P2Q2的距离为ns（0＜n＜1）时，电阻R上的热功率为：
P＝
＝
答：（1）mgr（2）（3）
练习册系列答案
相关题目
