题目内容
3. AB为竖直转轴,细绳AC和BC的结点C系一质量为m的小球,两绳能承担的最大拉力均为2.25mg,当AC和BC均拉直时∠ABC=90°,∠ACB=53°,BC=1.2m.ABC能绕竖直轴AB匀速转动,因而C球在水平面内做匀速圆周运动,求:
AB为竖直转轴,细绳AC和BC的结点C系一质量为m的小球,两绳能承担的最大拉力均为2.25mg,当AC和BC均拉直时∠ABC=90°,∠ACB=53°,BC=1.2m.ABC能绕竖直轴AB匀速转动,因而C球在水平面内做匀速圆周运动,求:(1)m的线速度增大为何值时,BC绳才刚好被拉直?(g取10m/s2)
(2)若m的速率继续增加,哪条绳先断,此时小球的速率多大?
分析 (1)当小球线速度增大时,BC逐渐被拉直,小球线速度增至BC刚被拉直时,对小球进行受力分析,合外力提供向心力,根据向心力公式求出C球速度;
(2)当小球线速度增大时,BC逐渐被拉直,小球线速度增至BC刚被拉直时,对小球进行受力分析,合外力提供向心力,求出A绳的拉力,线速度再增大些,TA不变而TB增大,所以BC绳先断.
解答 解:(1)当小球线速度增大时,BC逐渐被拉直,小球线速度增至BC刚被拉直时,
对球:TAsin∠ACB-mg=0…①
TAcos∠ACB+TB=m$\frac{{v}^{2}}{r}$…②
BC刚被拉直时TB=0
由①可求得AC绳中的拉力TA=$\frac{5}{4}$mg ③
由题知:r=BC
由②得:v=3m/s
(2)由上知线速度再增大些,TA不变而TB增大,所以BC绳先断.
当BC绳刚要断时,拉力为2.25mg
则代入②得:$\frac{5}{4}$mgcos53°+2.25mg=m$\frac{{v}^{2}}{1.2}$
解得:v=6m/s.
答:
(1)m的线速度增大为3m/s时,BC绳才刚好被拉直.
(2)若m的速率继续增加,BC绳先断,此时小球的速率为6m/s.
点评 解决本题的关键搞清向心力的来源,抓住临界状态的特点,运用牛顿第二定律进行求解.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
13. 如图所示,匀强磁场方向垂直线圈平面,先后两次将线框从同一位置匀速地拉出有界磁场.第一次速度为v1=v,第二次速度为v2=3v,在先后两次过程中( )
如图所示,匀强磁场方向垂直线圈平面,先后两次将线框从同一位置匀速地拉出有界磁场.第一次速度为v1=v,第二次速度为v2=3v,在先后两次过程中( )
 如图所示,匀强磁场方向垂直线圈平面,先后两次将线框从同一位置匀速地拉出有界磁场.第一次速度为v1=v,第二次速度为v2=3v,在先后两次过程中( )
如图所示,匀强磁场方向垂直线圈平面,先后两次将线框从同一位置匀速地拉出有界磁场.第一次速度为v1=v,第二次速度为v2=3v,在先后两次过程中( )| A. | 线框中感应电流之比为1:3 | |
| B. | 线框中产生热量之比为1:3 | |
| C. | 沿运动方向作用在线框上的外力的功率之比为1:3 | |
| D. | 流过任一截面电荷量之比为1:3 |
14.下列设备利用了电磁感应原理,从而极大地促进了社会生产力发展( )
| A. | 交流发电机 | B. | 电动机 | C. | 电饭锅 | D. | 电磁炉 |
18. 如图所示,水平细杆上套一环A,环A与球B间用一不可伸长轻质绳相连,质量分别为m1,和m2由于B球受到水平风力作用,A环与B球一起向右匀速运动,此时绳与竖直方向的夹角为θ,则下列说法中正确的是( )
如图所示,水平细杆上套一环A,环A与球B间用一不可伸长轻质绳相连,质量分别为m1,和m2由于B球受到水平风力作用,A环与B球一起向右匀速运动,此时绳与竖直方向的夹角为θ,则下列说法中正确的是( )
 如图所示,水平细杆上套一环A,环A与球B间用一不可伸长轻质绳相连,质量分别为m1,和m2由于B球受到水平风力作用,A环与B球一起向右匀速运动,此时绳与竖直方向的夹角为θ,则下列说法中正确的是( )
如图所示,水平细杆上套一环A,环A与球B间用一不可伸长轻质绳相连,质量分别为m1,和m2由于B球受到水平风力作用,A环与B球一起向右匀速运动,此时绳与竖直方向的夹角为θ,则下列说法中正确的是( )| A. | B球受到的风力为mgtanθ | |
| B. | 风力增大时,轻质绳对B球的拉力保持不变 | |
| C. | 风力增大时,杆对A球的支持力增大 | |
| D. | 风力增大时,杆对A球的摩擦力不变 |
15.质量不相等的甲、乙两物体,不计空气阻力,它们在同一高度处同时下落,则下列说法正确的是( )
| A. | 甲比乙先着地 | B. | 甲比乙的加速度大 | ||
| C. | 甲、乙同时着地 | D. | 甲比乙的加速度小 |
12.在研究平抛运动的实验中,下列说法正确的是( )
| A. | 为了描绘一条轨迹,每次应从同一位置释放小球 | |
| B. | 应该使斜槽末端的切线水平 | |
| C. | 坐标原点为小球即将离开斜槽时球心所在的位置 | |
| D. | 测定平抛初速时,应该取轨迹上离抛出点较远的点进行测量 |
 叶同学乔迁新居后,观察新家的电表如图所示,为了测试其是否准确,采用了如下方法:打开家中一盏“220V 100W”的电灯,将其它的电器全部关闭且不在待机状态,然后计时5分钟,若电表计电量准确,应该转动6圈.
叶同学乔迁新居后,观察新家的电表如图所示,为了测试其是否准确,采用了如下方法:打开家中一盏“220V 100W”的电灯,将其它的电器全部关闭且不在待机状态,然后计时5分钟,若电表计电量准确,应该转动6圈.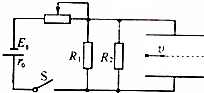 如图所示,电源电动势E=15V,内阻r=1Ω,电阻R1=30Ω,R2=60Ω.间距d=0.2m的两平行金属板水平放置.闭合开关S,板间电场视为匀强电场,一带正电的小球以某一速度沿两板间中线恰好匀速通过.设滑动变阻器接入电路的阻值为Rx=29Ω,忽略空气对小球的作用,取g=10m/s2.求:
如图所示,电源电动势E=15V,内阻r=1Ω,电阻R1=30Ω,R2=60Ω.间距d=0.2m的两平行金属板水平放置.闭合开关S,板间电场视为匀强电场,一带正电的小球以某一速度沿两板间中线恰好匀速通过.设滑动变阻器接入电路的阻值为Rx=29Ω,忽略空气对小球的作用,取g=10m/s2.求: 如图所示,有一个可视为质点的质量为m=1kg的小物块,从光滑平台上的A点以v0=1.8m/s的初速度水平抛出,到达C点时,恰好沿C点的切线方向进入固定在竖直平面内的光滑圆弧轨道,最后小物块无碰撞地滑上紧靠轨道末端D点的足够长的水平传送带.已知传送带上表面与圆弧轨道末端切线相平,传送带沿顺时针方向匀速运行的速度为v=3m/s,小物块与传送带间的动摩擦因数μ=0.5,圆弧轨道的半径为R=2m,C点和圆弧的圆心O点连线与竖直方向的夹角θ=53°,不计空气阻力,重力加速度g=10m/s2,sin53°=0.8、cos53°=0.6.求:
如图所示,有一个可视为质点的质量为m=1kg的小物块,从光滑平台上的A点以v0=1.8m/s的初速度水平抛出,到达C点时,恰好沿C点的切线方向进入固定在竖直平面内的光滑圆弧轨道,最后小物块无碰撞地滑上紧靠轨道末端D点的足够长的水平传送带.已知传送带上表面与圆弧轨道末端切线相平,传送带沿顺时针方向匀速运行的速度为v=3m/s,小物块与传送带间的动摩擦因数μ=0.5,圆弧轨道的半径为R=2m,C点和圆弧的圆心O点连线与竖直方向的夹角θ=53°,不计空气阻力,重力加速度g=10m/s2,sin53°=0.8、cos53°=0.6.求: