题目内容
【题目】如图所示,在![]() 平面的第一象限,存在以
平面的第一象限,存在以![]() 轴、
轴、![]() 轴、直线及直线
轴、直线及直线![]() 为边界的匀强电场区域I,电场强度大小为E,方向水平向右;在第二象限存在以
为边界的匀强电场区域I,电场强度大小为E,方向水平向右;在第二象限存在以![]() 轴、
轴、![]() 轴、
轴、![]() 及
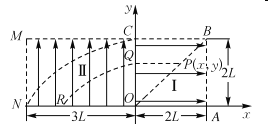
及![]() 边界的匀强电场区域II,电场方向竖直向上.一电子(电荷量大小为e,质量为m,不计重力)从B点处静止释放,恰好从N点离开电场区域II.
边界的匀强电场区域II,电场方向竖直向上.一电子(电荷量大小为e,质量为m,不计重力)从B点处静止释放,恰好从N点离开电场区域II.
(1)求电子通过C点时的速度大小;
(2)求电场区域II中的电场强度的大小.
(3)电子由电场区域I中某点静止释放,从电场域II的边界NO离开,且出射速度的方向与![]() 轴负方向成53°角,求释放点的位置应满足的条件(sin53°=0.8,cos53°=0.6).
轴负方向成53°角,求释放点的位置应满足的条件(sin53°=0.8,cos53°=0.6).

【答案】(1) ![]() (2)
(2) ![]() (3) 电子的释放点在一条直线段上,即y=x(0<x<2L)
(3) 电子的释放点在一条直线段上,即y=x(0<x<2L)
【解析】
(1)从B到C,依题意有
![]()
![]()
解得
![]()
(2)电子从C点进入电场区域Ⅱ,在区域Ⅱ中电子做类平拋运动,如图所示.
x轴方向:
3L=vC·t
y轴方向:
![]()
联立两式结合
![]()
解得
![]()
(3)电子由电场区域Ⅰ中某点P(x,y)静止释放、经Q点进入电场区域Ⅱ,并从R点离开,设vR与边界NO的夹角为θR. 于是有
![]() ,
,![]()

由题意易得
![]()
联立以上各式并带入数据得
y=x
故电子的释放点在一条直线段上,即
y=x(0<x<2L)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目









