题目内容
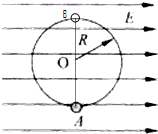 半径为R的绝缘光滑圆环固定在竖直平面内,环上套有一质量为m、带正电的珠子,空间存在水平向右的匀强电场,如图,珠子所受静电力是其重力的
半径为R的绝缘光滑圆环固定在竖直平面内,环上套有一质量为m、带正电的珠子,空间存在水平向右的匀强电场,如图,珠子所受静电力是其重力的| 3 |
| 4 |
(1)初速度VA至少多大才能使珠子做完整的圆周运动?(重力加速度为g)
(2)若初速度VA=
| 5gR |
分析:(1)根据共点力平衡得出珠子圆周运动的最高点,要使珠子做完整的圆周运动,在等效最高点速度为零,根据动能定理求出初速度的最小值.
(2)根据动能定理求出B点的速度,通过牛顿第二定律求出珠子受到环的作用力.
(2)根据动能定理求出B点的速度,通过牛顿第二定律求出珠子受到环的作用力.
解答:解:(1)设珠子平衡时,珠子与O点连线与竖直方向的夹角为 θ,
则 tanθ=
=
,θ=37°
珠子刚好做完整圆周运动,过C点速度 vC=0
由A到C,由动能定理:-mgR(1+cosθ)-qERsinθ=0-
mvA2
解得vA=
.
(2)从A→B运用动能定理得,-mg2R=
mvB2-
mvA′2
解得vB=
在B点:mg+NB=
解得NB=0.
答:(1)初速度VA至少为vA=
才能使珠子做完整的圆周运动.
(2)珠子受环作用力为0.

则 tanθ=
| qE |
| mg |
| 3 |
| 4 |
珠子刚好做完整圆周运动,过C点速度 vC=0
由A到C,由动能定理:-mgR(1+cosθ)-qERsinθ=0-
| 1 |
| 2 |
解得vA=
| 4.5gR |
(2)从A→B运用动能定理得,-mg2R=
| 1 |
| 2 |
| 1 |
| 2 |
解得vB=
| gR |
在B点:mg+NB=
| mvB2 |
| R |
解得NB=0.
答:(1)初速度VA至少为vA=
| 4.5gR |
(2)珠子受环作用力为0.
点评:解决本题的关键知道小球在竖直面内做圆周运动的等效最高点,抓住等效最高点的临界速度为零,结合动能定理进行求解.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
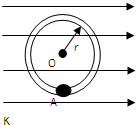 如图所示,半径为r的绝缘光滑圆环固定在竖直平面内,环上套有一个质量为m、带正电的珠子,空间存在水平向右的匀强电场,珠子所受的电场力是其重力的
如图所示,半径为r的绝缘光滑圆环固定在竖直平面内,环上套有一个质量为m、带正电的珠子,空间存在水平向右的匀强电场,珠子所受的电场力是其重力的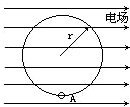 半径为r的绝缘光滑圆环固定在竖直平面内,环上套有一质量为m、带正电的珠子,空间存在水平向右的匀强电场,如图所示.珠子所受静电力是其重力的
半径为r的绝缘光滑圆环固定在竖直平面内,环上套有一质量为m、带正电的珠子,空间存在水平向右的匀强电场,如图所示.珠子所受静电力是其重力的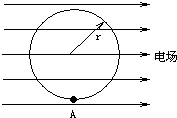 (2007?淮安模拟)半径为r的绝缘光滑圆环固定在竖直平面内,环上套有一质量为m、带正电的珠子,空间存在水平向右的匀强电场,如图所示.珠子所受静电力是其重力的3/4倍.将珠子从环上最低位置A点静止释放,求:
(2007?淮安模拟)半径为r的绝缘光滑圆环固定在竖直平面内,环上套有一质量为m、带正电的珠子,空间存在水平向右的匀强电场,如图所示.珠子所受静电力是其重力的3/4倍.将珠子从环上最低位置A点静止释放,求: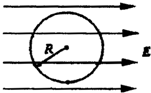 半径为R的绝缘光滑圆环固定在竖直平面内,环上套有一个带正的小珠子,该装置所在空间存在着水平向右的匀强电场,如图,已知珠子所受电场力是重力的3/4倍,将珠子从最低点由静止释放,则珠子获得的最大速度是
半径为R的绝缘光滑圆环固定在竖直平面内,环上套有一个带正的小珠子,该装置所在空间存在着水平向右的匀强电场,如图,已知珠子所受电场力是重力的3/4倍,将珠子从最低点由静止释放,则珠子获得的最大速度是 半径为r的绝缘光滑圆环固定在竖直平面内,环上套有一质量为m,带正电的珠子,空间存在水平向右的匀强电场,如图所示,珠子所受静电力是其重力的3/4,将珠子从环上最低位置A点由静止释放,则珠子所能获得的最大动能Ek为( )
半径为r的绝缘光滑圆环固定在竖直平面内,环上套有一质量为m,带正电的珠子,空间存在水平向右的匀强电场,如图所示,珠子所受静电力是其重力的3/4,将珠子从环上最低位置A点由静止释放,则珠子所能获得的最大动能Ek为( )