Question

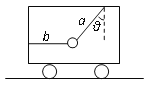
【题目】如图所示，质量M = 1kg的木板静止在粗糙的水平地面上，木板与地面间的动摩擦因数μ1=0.1，在木板的左端放置一个质量m=1kg、大小可以忽略的铁块，铁块与木板间的动摩擦因数μ2=0.4，试求：

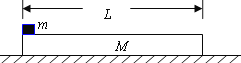
（1）若木板长L=1m，在铁块上加一个水平向右的恒力F=8N，经过多长时间铁块运动到木板的右端？

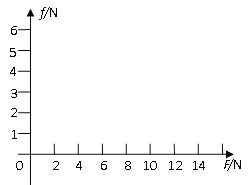
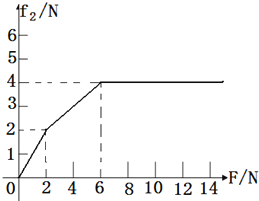
（2）若在木板（足够长）的右端施加一个大小从零开始连续增加的水平向左的力F，通过分析和计算后，请在图中画出铁块受到的摩擦力f随拉力F大小变化的图像。

Answer 1

【答案】（1） t=1s

（2）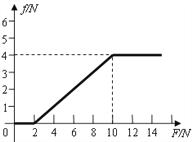

【解析】

（1）假设相对滑动，则根据牛顿第二定律得，铁块的加速度大小
；
木块的加速度大小 ．
由a2＞0可见 假设成立．
设经过时间t铁块运动到木块的右端，则有 a1t2a2t2＝L，
解得 t=1s
（2）①当F≤μ1（M+m）g=2N时，m、M相对静止且对地静止，有：f2=F；
②设F=F1时，m、M恰保持相对静止，此时系统的加速度为：a=a2=2m/s2．
以系统为研究对象，据牛顿第二定律有：F1-μ1（M+m）g=（M+m）a，
解得：F1=6N
所以，当2N＜F≤6N时，m、M相对静止，系统向右做匀加速运动，
其加速度：

以M为研究对象，据牛顿第二定律有：f2-μ1（M+m）g=Ma
解得：

③当F＞6N时，m、M发生相对运动有：f2=μ2mg=4N
所以，f2随拉力F大小的变化而变化的图象如图所示．