题目内容
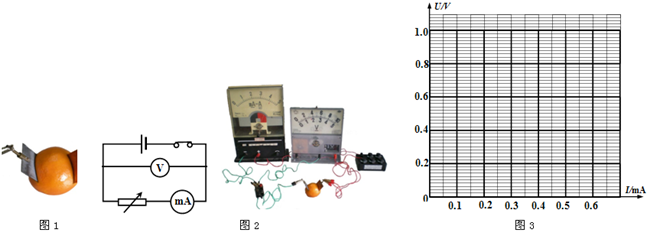
(1)利用图1所示的电路测量电流表的内阻RA.图中R1、R2为电阻,K1、K2为电键,B是电源(内阻可忽略).
①根据图1所给出的电路原理图,在图2的实物图上连线.
②已知R1=140Ω,R2=60Ω.当电键K1闭合、K2断开时,电流表读数为6.4mA;当K1、K2均闭合时,电流表读数为8.5mA.由此可以求出RA=______Ω.
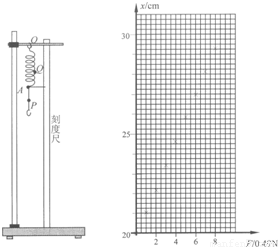
(2)将弹簧的上端O点固定悬吊在铁架台上,旁边置一刻度尺,刻度尺的零刻线跟O点对齐,在弹簧的下部A处做一标记,如固定一个指针.在弹簧下端的挂钩上挂上钩码(每个钩码的质量都是50g),指针在刻度尺上指示的刻度x.逐个增加所挂钩码的个数,刻度x随挂钩上的钩码的重量F而变化,几次实验测得相应的F、x各点描绘在图中.
①请在图中描绘出x随F变化的图象.
②由图象得出弹簧的劲度系数kA=______ N/m.(结果取2位有效数字).
③此弹簧的弹力大小F弹跟弹簧伸长△x的关系是______.
④如果将指针固定在A点的下方P处,再做出x随F变化的图象,得出弹簧的劲度系数与k相比,可能是______
A.大于kA B.等于kA
C.小于kA D.无法确定
⑤如果将指针固定在A点的上方Q处,再做出x随F变化的图象,得出弹簧的劲度系数与k相比,可能是______
A.大于kA B.等于kA
C.小于kA D.无法确定.
【答案】分析:(1)根据电路图连接实物图,按照一个一个回路去连,否则会出现凌乱;运用两种状态下电路图,根据闭合电路欧姆定律列出方程组,从而即可求解;
(2)根据胡克定律在弹簧的弹性限度内,弹力的大小与弹簧的形变量成正比,所以每挂一个钩码拉力增加量相同,弹簧的增加的长度也相同;作图过程中根据胡克定律在弹簧的弹性限度内,弹力的大小与弹簧的形变量成正比,可知画出弹簧弹力F与其伸长量x间关系的F-x图象应为一条倾斜直线.根据F-x图象解斜率即可得到劲度系数.
解答:解:(1)①根据实验原理图连接实物图如下所示:

②根据闭合电路欧姆定律可得:
当电键K1闭合、K2断开时,E=I1(R1+RA+R2)
当K1、K2均闭合时,E=I2(R1+RA)
将数据代入解得:RA=42.8Ω
故答案为:①如上图;②42.8Ω.
(2)①x随F变化的图象如下所示:
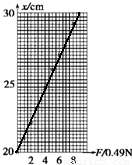
②由胡克定律:F=kx可知图象的斜率倒数表示劲度系数,
所以由图象可以解出劲度系数k=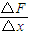 =32N/m
=32N/m
③弹簧的弹力大小F跟弹簧伸长量△x的关系是F=32△x.
④如果将指针固定在A点的下方P处,弹簧的劲度系数不变,得出弹簧的劲度系数仍等于kA,故B正确.
⑤如果将指针固定在A点的上方Q处,由于选用的弹簧变短,则弹簧的劲度系数变大,得出弹簧的劲度系数与kA相比,要大于kA,故A正确.
故答案为:①见上图;②32,③F=32△x,④B,⑤A.
点评:(1)学会电路图与实物图相互转换,同时运用闭合电路欧姆定律来列式求解.注意结果保留有效数字;
(2)应用胡克定律注意弹簧的形变量既可以是弹簧的伸长量又可以是压缩量,解题时注意弹簧是被拉长还是被压缩.
(2)根据胡克定律在弹簧的弹性限度内,弹力的大小与弹簧的形变量成正比,所以每挂一个钩码拉力增加量相同,弹簧的增加的长度也相同;作图过程中根据胡克定律在弹簧的弹性限度内,弹力的大小与弹簧的形变量成正比,可知画出弹簧弹力F与其伸长量x间关系的F-x图象应为一条倾斜直线.根据F-x图象解斜率即可得到劲度系数.
解答:解:(1)①根据实验原理图连接实物图如下所示:

②根据闭合电路欧姆定律可得:
当电键K1闭合、K2断开时,E=I1(R1+RA+R2)
当K1、K2均闭合时,E=I2(R1+RA)
将数据代入解得:RA=42.8Ω
故答案为:①如上图;②42.8Ω.
(2)①x随F变化的图象如下所示:

②由胡克定律:F=kx可知图象的斜率倒数表示劲度系数,
所以由图象可以解出劲度系数k=
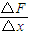 =32N/m
=32N/m③弹簧的弹力大小F跟弹簧伸长量△x的关系是F=32△x.
④如果将指针固定在A点的下方P处,弹簧的劲度系数不变,得出弹簧的劲度系数仍等于kA,故B正确.
⑤如果将指针固定在A点的上方Q处,由于选用的弹簧变短,则弹簧的劲度系数变大,得出弹簧的劲度系数与kA相比,要大于kA,故A正确.
故答案为:①见上图;②32,③F=32△x,④B,⑤A.
点评:(1)学会电路图与实物图相互转换,同时运用闭合电路欧姆定律来列式求解.注意结果保留有效数字;
(2)应用胡克定律注意弹簧的形变量既可以是弹簧的伸长量又可以是压缩量,解题时注意弹簧是被拉长还是被压缩.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
 分享到
分享到- QQ空间
- 新浪微博
- 百度搜藏
- 人人网
- 腾讯微博
- 开心网
- 腾讯朋友
- 百度空间
- 豆瓣网
- 搜狐微博
- MSN
- QQ收藏
- 我的淘宝
- 百度贴吧
- 搜狐白社会
- 更多...
百度分享
一个有一定厚度的圆盘,可以绕通过中心垂直于盘面的水平轴转动,用下面的方法测量它匀速转动时的角速度。
实验器材:电磁打点计时器、米尺、纸带、复写纸片。
实验步骤:
(1)如图1所示,将电磁打点计时器固定在桌面上,将纸带的一端穿过打点计时器的限位孔后,固定在待测圆盘的侧面上,使得圆盘转动时,纸带可以卷在圆盘侧面上。
(2)启动控制装置使圆盘转动,同时接通电源,打点计时器开始打点。
(3)经过一段时间,停止转动和打点,取下纸带,进行测量。
① 由已知量和测得量表示的角速度的表达式为ω= 。式中各量的意义是:
.
② 某次实验测得圆盘半径r=5.50×10-2m,得到纸带的一段如图2所示,求得角速度为 。
(1) (2)6.8/s。 |




 =
= 
















