题目内容
如图,顶角为90°的“∨”型光滑金属导轨MON固定在倾角为θ的绝缘斜面上,M、N连线平行于斜面底端,导轨MO、NO的长度相等,M、N两点间的距离L=2m,整个装置处于磁感应强度大小B=0.5T、方向垂直于斜面向下的匀强磁场中。一根质量m=0.4kg,粗细均匀、单位长度电阻值r=0.5Ω/m的导体棒ab,受到平行于斜面向上且垂直于ab的变力F作用,以速度v=2m/s沿导轨向下匀速滑动,导体棒在运动过程中始终与导轨接触良好,不计导轨电阻,从导体棒在MN时开始计时,

⑴t=0时,F=0,求斜面倾角θ;
⑵求0.2s内通过导体棒的电荷量q;
⑶求导体棒通过整个金属导轨的过程中产生的焦耳热Q。

⑴t=0时,F=0,求斜面倾角θ;
⑵求0.2s内通过导体棒的电荷量q;
⑶求导体棒通过整个金属导轨的过程中产生的焦耳热Q。
(1)300(2)0.4C(3)1J
试题分析:⑴导体棒开始运动时,回路中产生的感应电动势E=BL v
感应电流

安培力F安=BIL
由平衡条件得:mgsinθ=F安 +F
F=0
联立上式得:θ=300
⑵感应电流
 与导体棒切割的有效长度l无关
与导体棒切割的有效长度l无关感应电流大小
 A
A 故0.2s内通过导体棒的电荷量q=It=0.4C
⑶解法(一)设导体棒经t时间沿导轨匀速向下运动的位移为x,
则t时刻导体棒切割的有效长度Lx= L-2x
导体棒在导轨上运动时所受的安培力

因安培力的大小
 与位移x成线性关系,故通过导轨过程中导体棒所受安培力的平均值
与位移x成线性关系,故通过导轨过程中导体棒所受安培力的平均值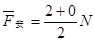

产生的焦耳热Q


点评:本题考察了电磁感应问题中常见的安培力等求法,在功能关系中,由于安培力线性变化,所以类似于弹簧弹力做功求法找到安培力做功的方法。也可以尝试用图象法求解。

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目










 =30°、宽度L=1m的足够长的U形平行光滑金属导轨固定在磁感应强度B=1T、范围充分大的匀强磁场中,磁场方向垂直导轨平面斜向上.现用一平行导轨的牵引力F,牵引一根质量m=0.2kg、电阻R=1
=30°、宽度L=1m的足够长的U形平行光滑金属导轨固定在磁感应强度B=1T、范围充分大的匀强磁场中,磁场方向垂直导轨平面斜向上.现用一平行导轨的牵引力F,牵引一根质量m=0.2kg、电阻R=1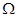 、垂直导轨的金属棒ab,由静止沿导轨向上移动(ab棒始终与导轨接触良好且垂直,不计导轨电阻及一切摩擦)。问:
、垂直导轨的金属棒ab,由静止沿导轨向上移动(ab棒始终与导轨接触良好且垂直,不计导轨电阻及一切摩擦)。问:
