题目内容
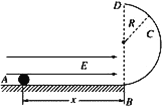
【题目】如图甲所示,在真空中,半径为R的圆形区域内存在匀强磁场,磁场方向垂直纸面向外。在磁场左侧有一对平行金属板M、N,两板间距离也为R,板长为L,板的中心线O1O2与磁场的圆心O在同一直线上。置于O1处的粒子发射源可连续以速度v0沿两板的中线O1O2发射电荷量为q、质量为m的带正电的粒子(不计粒子重力),MN两板不加电压时,粒子经磁场偏转后恰好从圆心O的正下方P点离开磁场;若在M、N板间加如图乙所示交变电压UMN,交变电压的周期为![]() ,t=0时刻入射的粒子恰好贴着N板右侧射出。求
,t=0时刻入射的粒子恰好贴着N板右侧射出。求

(1)匀强磁场的磁感应强度B的大小
(2)交变电压电压U0的值
(3)若粒子在磁场中运动的最长、最短时间分别为t1 、t 2 ,则它们的差值![]() 为多大?
为多大?
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
试题分析:(1)当UMN=0时粒子沿O2O3方向射入磁场轨迹如图⊙O1,设其半径为R1 。
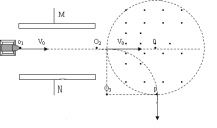
由几何关系得:R1=R

解得:![]()
(2)在t=0时刻入射粒子满足:
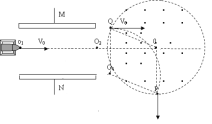
![]()
解得: ![]()
(3)经分析可知所有粒子经电场后其速度仍为![]() ,
,
当![]() (k=0,1,2,3. )时刻入射的粒子贴M板平行射入磁场轨迹如⊙04,偏转角为
(k=0,1,2,3. )时刻入射的粒子贴M板平行射入磁场轨迹如⊙04,偏转角为![]() 。
。
由几何知识可知四边形QOPO4为菱形,故![]()
![]()
当![]() (k=0,1,2,3. )时刻入射的粒子贴N板平行射入磁场轨迹如⊙05 偏转角为
(k=0,1,2,3. )时刻入射的粒子贴N板平行射入磁场轨迹如⊙05 偏转角为![]() 。
。
由几何知识可知SOPO5为菱形,故![]()
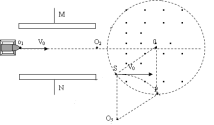
![]()
又 ![]()
故 ![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目