题目内容
固定光滑细杆与地面成一定倾角θ,在杆上套有一个光滑小环,小环在沿杆方向向上的力F作用下向下运动,作用力F的大小与小环速度v的大小随时间变化规律如图所示,重力加速度g取10m/s2求: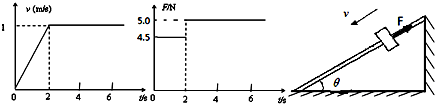
(1)前2s小环的加速度大小a
(2)小环的质量m和细杆与地面间的倾角θ

(1)前2s小环的加速度大小a
(2)小环的质量m和细杆与地面间的倾角θ
分析:从速度时间图象得到小环的运动规律,即先加速和匀速,求出加速度,得到合力,然后受力分析,根据共点力平衡条件和牛顿第二定律列式求解;同样可以得出细杆与地面的倾角α.
解答:解:由图得:a=
=
=0.5m/s2
前2s,F=F1=4.5N,根据牛顿第二定律得
mgsinθ-F1=ma ①
2s后物体做匀速运动,F=F2=5N
根据共点力平衡条件有:mgsinθ=F2 ②
联立①②可得:m=1kg
θ=30°
答:(1)前2s小环的加速度大小为0.5m/s2,(2)小环的质量m和细杆与地面间的倾角为30°.
| v |
| t |
| 1 |
| 2 |
前2s,F=F1=4.5N,根据牛顿第二定律得
mgsinθ-F1=ma ①
2s后物体做匀速运动,F=F2=5N
根据共点力平衡条件有:mgsinθ=F2 ②
联立①②可得:m=1kg
θ=30°
答:(1)前2s小环的加速度大小为0.5m/s2,(2)小环的质量m和细杆与地面间的倾角为30°.
点评:本题关键是分析小环的运动情况,先加速后匀速,然后受力分析,根据共点力平衡和牛顿第二定律列式求解.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目




