题目内容
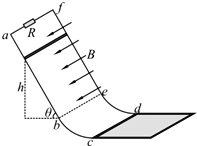
【题目】如图所示，光滑导轨abc与fed相距
，其中ab、fe段是倾角
的直轨道，bc、ed段是半径
的圆弧轨道且与ab、fe相切，轨道末端c、d点切线与一放置在光滑水平地面上、质量
的木板上表面平滑连接。在abef间有垂直于轨道平面向下、
的匀强磁场，定值电阻
把质量为
、电阻不计的金属杆从距b、e高
的导轨上静止释放，杆在直轨道上先加速后匀速下滑。如果杆与木板间摩擦因数
，取
，求：
(1)杆由静止下滑到cd的过程中R上产生的焦耳热Q；
(2)杆运动到cd时对轨道的压力F大小；
(3)要使杆不从木板上掉下的木板最小长度s。
【答案】 
；
25N 
【解析】
据题意，杆在直轨道上先加速后匀速下滑，到达be前已经匀速运动，根据平衡条件和安培力与速度的关系式，可求出匀速运动的速度，由动能定理研究杆从be到cd的过程，求得杆经过cd处的速度大小，由牛顿第二定律、第三定律求解杆对轨道的压力。再根据能量守恒定律求出R上产生的焦耳热。杆滑上木板后做匀减速运动，木板做匀加速运动，当杆与木板的速度相等时，杆刚好不能滑出木板，此时木板的长度最小，由牛顿第二定律、运动学公式和位移关系求解s。
设杆滑到be处时速度为
，由题意知此时杆匀速下滑，有：
①
②
③
由①②③联立得：
④
由能量守恒：
⑤
则得：
⑥
（2）设杆滑到cd处时速度为
，杆受到轨道支持力为
，由动能定理有：
⑦
cd处：
⑧
由牛顿第三定律：
⑨
联解④⑦⑧⑨得：
⑩
（3）由⑦得：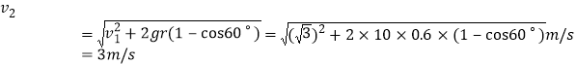
杆滑上木板后，杆与木板在相互间摩擦力作用下运动，设经过时间t共同运动，则：
对杆：
，
(11)
对木板：
，
(12)
共同运动时有：
(13)
则得：
（14）
此过程杆的位移
(15)
木板的位移
(16)
则有木板最小长度
(17)
练习册系列答案
相关题目
