��Ŀ����
����Ŀ��ˮ�ϻ��ݿɼ���ͼ��ʾ��ģ�ͣ�б��AB�⻬Բ����BCƽ�����ӣ�б��AB����ֱ�߶�H=6.0m����Ǧ�=37�㣮Բ��BC�뾶R=3.0m��ĩ��C�������ˮƽ��C����ˮƽ��ľ���h=0.80m������AB��Ķ�Ħ������Ϊ��=0.2��ȡ�������ٶ�g=10m/s2 �� cos37��=0.8��sin37��=0.6��һ������m=30kg��С���Ѵӻ��ݶ���A�����ٵ����ɻ��£���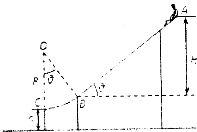
��1��С������б��AB�»�ʱ���ٶ�a�Ĵ�С��
��2��С���ѻ���C��ʱ�ٶ�v�Ĵ�С����C��ʱ�ܵ������ѹ��Fc�Ĵ�С��
��3���ڴ�C�㻬�����䵽ˮ��Ĺ����У�С������ˮƽ����λ��x�Ĵ�С��
���𰸡�
��1���⣺С������б��AB�»�����ţ�ٵڶ�����֪��mgsin�ȩ���mgcos��=ma
���a=4.4m/s2��
��С������б��AB�»�ʱ���ٶ�a�Ĵ�СΪ4.4m/s2��
��2���⣺�� ![]() �����С���ѻ���B����ٶ�
�����С���ѻ���B����ٶ� ![]()
��B��C���ɶ��ܶ����ã� ![]()
��ã�v=10m/s��
����C��ʱ����ţ�ٵڶ����ɣ� ![]()
���FC=1300N
����ţ�ٵ������ɣ�С���ѶԲ����ѹ��FC��=FC=1300N��
��С���ѻ���C��ʱ�ٶ�v�Ĵ�С����C��ʱ�ܵ������ѹ��Fc�Ĵ�СΪ1300N��
��3���⣺�ڴ�C�㻬�����䵽ˮ��Ĺ����У�С������ƽ���˶���
�� ![]() �ã�t=0.4s��
�ã�t=0.4s��
��ˮƽ�����ϵ�λ��x=vt=4m��
���ڴ�C�㻬�����䵽ˮ��Ĺ����У�С������ˮƽ����λ��x�Ĵ�СΪ4m��
����������1����С���ѽ�����������������ţ�ٵڶ����ɿ�����»�ʱ�ļ��ٶȣ�
��2��ѡȡС���Ѵ�A����C�Ĺ��̣����Ը��ݶ��ܶ������C����ٶȣ�
��3����C�㻬��ʱ��С������ƽ���˶������Ը��ݸ߶�����˶���ʱ�䣬�ٸ���ˮƽ����������ֱ���˶����ˮƽλ�ƣ�
�����㾫����ͨ���������ƽ���˶��Ͷ��ܶ������ۺ�Ӧ�ã������ص�:�پ���ˮƽ����ij��ٶ�;��ֻ���������ã��Ǽ��ٶ�Ϊ�������ٶ�g���ȱ��������˶����˶�����:ƽ���˶����Էֽ�Ϊˮƽ���������ֱ���˶�����ֱ��������������˶���Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ�ݼ����Խ����⣮






