题目内容
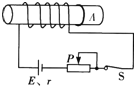
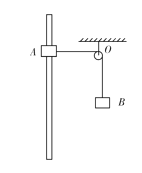
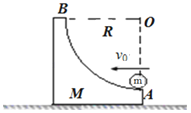
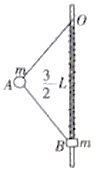
【题目】一转动装置如图所示,两根轻杆OA和AB与一小球以及一小环通过铰链连接,两轻杆长度相同,球和环的质量均为m,O端通过铰链固定在竖直的轻质转轴上,套在转轴上的轻质弹簧连接在O与小环之间,原长为L,装置静止时,弹簧长为![]() L,转动该装置并缓慢增大转速,小环缓慢上升。弹簧始终在弹性限度内,忽略一切摩擦和空气阻力,重力加速度为g,求:
L,转动该装置并缓慢增大转速,小环缓慢上升。弹簧始终在弹性限度内,忽略一切摩擦和空气阻力,重力加速度为g,求:
(1)弹簧的劲度系数k;
(2)AB杆中弹力为零时,装置转动的角速度![]() 0。
0。
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)装置静止时,设OA、OB杆中的弹力分别为F1、T1,OA杆与转轴的夹角为![]() 1,小环受到的弹力
1,小环受到的弹力
F弹1=k![]()
小环受力平衡有
F弹1=mg+T1![]()
小球受力平衡有
F1![]() + T1
+ T1![]() =mg
=mg
F1![]() = T1
= T1![]()
解得弹簧的劲度系数
k=![]()
(2)设OA杆中的弹力为F2,OA杆与转轴的夹角为![]() 2,弹簧长度为x,轻杆长度为l,小环受到弹簧的弹力
2,弹簧长度为x,轻杆长度为l,小环受到弹簧的弹力
F弹2=k(x-L)
小环受力平衡
F弹2=mg
解得AB杆中弹力为零时,弹簧的长度
x=![]() L
L
则![]() =
=![]() ,对小球竖直方向有
,对小球竖直方向有
F2![]() =mg
=mg
对小球,根据牛顿第二定律
F2![]() =m
=m![]() 20l
20l![]()
解得AB杆中弹力为零时,装置转动的角速度
![]() 0=
0=![]()
即弹簧的劲度系数k=![]() ;AB杆中弹力为零时,装置转动的角速度
;AB杆中弹力为零时,装置转动的角速度![]() 0=
0=![]() 。
。

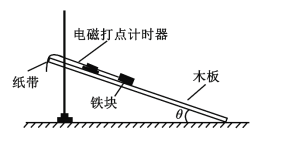
【题目】某同学用如图甲所示装置验证动量守恒定律。主要实验步骤如下:
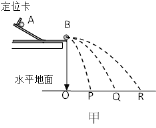
(ⅰ)将斜槽固定在水平桌面上,调整末端切线水平;
(ⅱ)将白纸固定在水平地面上,白纸上面放上复写纸;
(ⅲ)用重锤线确定斜槽末端在水平地面上的投影点O;
(ⅳ)让小球A紧贴定位卡由静止释放,记录小球的落地点,重复多次,确定落点的中心位置Q;
(ⅴ)将小球B放在斜槽末端,让小球A紧贴定位卡由静止释放,记录两小球的落地点,重复多次,确定A、B两小球落点的中心位置P、R;
(ⅵ)用刻度尺测量P、Q、R距O点的距离x1、x2、x3;
(ⅶ)用天平测量小球A、B质量m1、m2;
(ⅷ)分析数据,验证等式m1x2=m1x1+m2x3是否成立,从而验证动量守恒定律。
请回答下列问题
(1) 步骤(ⅴ)与步骤(ⅳ)中定位卡的位置应_____________;
(2)步骤(ⅶ)用天平测得A的质量为17.0 g。测量小球B的质量时将小球B放在天平的__盘,__盘放上一个5 g砝码,游码如图乙位置时天平平衡;


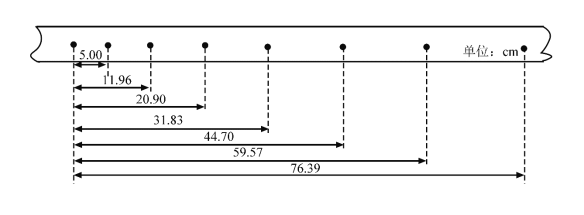
(3)如图丙是步骤(ⅵ)的示意图。该同学为完成步骤(ⅷ)设计了下列表格,并进行了部分填写,请将其补充完整①_______②_________③___________。
物理量 | 碰前 | 碰后 |
m/g | m1=17.0 | m1=17.0 m2= ① |
x/cm | x2=50.35 | x1= ② x3=74.75 |
mx/g·cm | m1x2=855.95 | m1x1+m2x3= ③ |