题目内容
一个质量为m的物体，以某一初速度冲上倾角为θ的斜面，沿斜面上滑，然后又下滑回到斜面底端．已知物体从最高点下滑到斜面底端的时间为由底端上滑到最高点时间的2倍，则物体与斜面间的动摩擦因数为________．
0.6tanθ
分析：物体初上斜面的过程可以反过来看成初速度为零的匀加速直线运动，根据牛顿第二定律求出两次运动的加速度，而两次运动的位移相等，根据位移时间公式即可求解．
解答：向上运动时的加速度大小为：a1=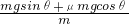
=g（sinθ+μcosθ）
向下滑时的加速度大小为a2=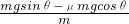
=g（sinθ-μcosθ）
设上滑的位移为x，则有：
上滑时x=
a1t12…①
下滑时x=a2t22…②
又因为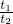
=0.5…③
由①②③解得：μ=0.6tanθ
故答案为：0.6tanθ
点评：本题主要考查了牛顿第二定律及运动学基本公式的直接应用，难度不大，属于基础题．
分析：物体初上斜面的过程可以反过来看成初速度为零的匀加速直线运动，根据牛顿第二定律求出两次运动的加速度，而两次运动的位移相等，根据位移时间公式即可求解．
解答：向上运动时的加速度大小为：a1=
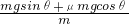=g（sinθ+μcosθ）向下滑时的加速度大小为a2=
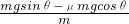=g（sinθ-μcosθ）设上滑的位移为x，则有：
上滑时x=
a1t12…①下滑时x=
a2t22…②又因为
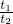=0.5…③由①②③解得：μ=0.6tanθ
故答案为：0.6tanθ
点评：本题主要考查了牛顿第二定律及运动学基本公式的直接应用，难度不大，属于基础题．
练习册系列答案
相关题目
（2011?徐汇区模拟）如图（a）所示，在倾角为37°的斜面上，一个质量为m的物体A在沿斜面向下的不同的恒定拉力F作用下从静止开始运动，设沿斜面向下的方向为正方向，物体A的加速度a与拉力F的关系如图（b）所示，则物体A的质量m为
如图所示，一个粗糙的水平转台以角速度ω匀速转动，转台上有一个质量为m的物体，物体与转台问用长L的绳连接着，此时物体与转台处于相对静止，设物体与转台间的动摩擦因数为μ，现突然制动转台，则（ ）
（2009?丰台区模拟）如图所示，一个质量为m的物体沿固定斜面匀速滑下，以下说法正确的是（ ）
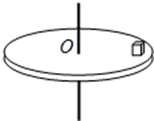如图所示，一圆盘可绕通过其中心且垂直于盘面的竖直轴转动，盘上距中心r处放置一个质量为m的物体，物体与盘面间滑动摩擦因数为μ，重力加速度为g．一段时间内观察到圆盘以角速度ω做匀速转动，物体随圆盘一起（相对静止）运动．这段时间内（ ）| A、物体受到圆盘对它的摩擦力，大小一定为μmg，方向与物体线速度方向相同 | B、物体受到圆盘对它的摩擦力，大小一定为mω2r，方向指向圆盘中心 | C、物体受到圆盘对它的摩擦力，大小可能小于μmg，方向指向圆盘中心 | D、物体受到圆盘对它的摩擦力，大小可能小于mω2r，方向背离圆盘中心 |