题目内容
13. 测定木块与长木板之间的动摩擦因数时,采用如图1所示的装置,图中长木板水平固定.
测定木块与长木板之间的动摩擦因数时,采用如图1所示的装置,图中长木板水平固定.(1)实验过程中,电火花计时器应接在交流(选填“直流”或“交流”)电源上.调整定滑轮高度,使细线与长木板平行.
(2)已知重力加速度为g,测得木块的质量为M,砝码盘和砝码的总质量为m,木块的加速度为a,则木块与长木板间动摩擦因数μ=$\frac{{mg-({m+M})a}}{Mg}$(用字母M、m、a、g表示).
(3)如图2为木块在水平木板上带动纸带运动打出的一条纸带的一部分,0、1、2、3、4、5、6为计数点,相邻两计数点间还有4个打点未画出.从纸带上测出x1=3.20cm,x2=4.52cm,x5=8.42cm,x6=9.70cm.则木块在计数点1处的速度大小v=0.39m/s,整个过程中的加速度大小a=1.3 m/s2(已知交流电频率f=50Hz,结果保留两位有效数字).

分析 了解实验仪器的使用和注意事项.
对木块、砝码盘和砝码进行受力分析,运用牛顿第二定律求出木块与长木板间动摩擦因数.
利用匀变速直线运动的推论,可计算出打出某点时纸带运动的加速度.
解答 解:(1)电火花计时器应接在交流电源上.调整定滑轮高度,使细线与长木板平行.
(2)对木块、砝码盘和砝码进行受力分析,
运用牛顿第二定律得:
对木块:F-μMg=Ma
对砝码盘和砝码:mg-F=ma
由上式得:μ=$\frac{{mg-({m+M})a}}{Mg}$;
(3)相邻两计数点间还有4个打点未画出,所以相邻的计数点之间的时间间隔为0.1s
根据平均速度等于中时刻的瞬时速度,则有:v1=$\frac{{x}_{1}+{x}_{2}}{2T}$=$\frac{0.032+0.0452}{2×0.1}$≈0.39m/s;
根据运动学公式得:△x=at2,
a=$\frac{0.0842+0.097-0.032-0.0452}{2×(2×0.1)^{2}}$≈1.3m/s2.
故答案为:(1)交流,细线与长木板平行;(2)$\frac{{mg-({m+M})a}}{Mg}$;(3)0.39,1.3.
点评 能够从物理情境中运用物理规律找出物理量间的关系.
要注意单位的换算和有效数字的保留.

练习册系列答案
相关题目
18. 如图所示,A、B、C三个不同的位置向右分别以vA、vB、vC的水平初速度抛出三个小球A、B、C,其中A、B在同一竖直线上,B、C在同一水平线上,三个小球均同时落在地面上的D点,不计空气阻力.则必须( )
如图所示,A、B、C三个不同的位置向右分别以vA、vB、vC的水平初速度抛出三个小球A、B、C,其中A、B在同一竖直线上,B、C在同一水平线上,三个小球均同时落在地面上的D点,不计空气阻力.则必须( )
 如图所示,A、B、C三个不同的位置向右分别以vA、vB、vC的水平初速度抛出三个小球A、B、C,其中A、B在同一竖直线上,B、C在同一水平线上,三个小球均同时落在地面上的D点,不计空气阻力.则必须( )
如图所示,A、B、C三个不同的位置向右分别以vA、vB、vC的水平初速度抛出三个小球A、B、C,其中A、B在同一竖直线上,B、C在同一水平线上,三个小球均同时落在地面上的D点,不计空气阻力.则必须( )| A. | 先同时抛出A、B两球,再抛出C球 | B. | 先同时抛出B、C两球,再抛出A球 | ||
| C. | 必须满足vA>vB>vC | D. | 必须满足vA<vB<vC |
5. 一个正点电荷Q静止在正方形的一个顶点上,另一个带电质点射入该区域时,仅受电场力的作用恰好能依次经过正方形的另外三个顶点a、b、c,如图所示,则有( )
一个正点电荷Q静止在正方形的一个顶点上,另一个带电质点射入该区域时,仅受电场力的作用恰好能依次经过正方形的另外三个顶点a、b、c,如图所示,则有( )
 一个正点电荷Q静止在正方形的一个顶点上,另一个带电质点射入该区域时,仅受电场力的作用恰好能依次经过正方形的另外三个顶点a、b、c,如图所示,则有( )
一个正点电荷Q静止在正方形的一个顶点上,另一个带电质点射入该区域时,仅受电场力的作用恰好能依次经过正方形的另外三个顶点a、b、c,如图所示,则有( )| A. | 质点在a、b、c三处的加速度大小之比是1:2:1 | |
| B. | 质点由a到b电势能减小,由b到.电场力做负功,在b点动能最小 | |
| C. | a、b、c三点电势高低及电场强度大小的关系是φa=φc>φb,Ea=Ec=2Eb | |
| D. | 若改变带电质点在a处的速度大小和方向,有可能使其在该电场中做类平抛运动 |
3. 如图所示,一架轰炸机在高度H=2155m的高空沿水平方向匀速飞行,在倾斜角度为θ=37°的山坡上方某一位置,先后自由释放两枚炸弹.其中先释放的炸弹正好垂直于斜面落在半山腰上的A点,后释放的炸弹正好落在山顶上的B点,落地点速度方向与山坡所在的面向上方向成74°角.不计空气阻力,g=10m/s2,sin37°=0.6,则下列判断正确的是( )
如图所示,一架轰炸机在高度H=2155m的高空沿水平方向匀速飞行,在倾斜角度为θ=37°的山坡上方某一位置,先后自由释放两枚炸弹.其中先释放的炸弹正好垂直于斜面落在半山腰上的A点,后释放的炸弹正好落在山顶上的B点,落地点速度方向与山坡所在的面向上方向成74°角.不计空气阻力,g=10m/s2,sin37°=0.6,则下列判断正确的是( )
 如图所示,一架轰炸机在高度H=2155m的高空沿水平方向匀速飞行,在倾斜角度为θ=37°的山坡上方某一位置,先后自由释放两枚炸弹.其中先释放的炸弹正好垂直于斜面落在半山腰上的A点,后释放的炸弹正好落在山顶上的B点,落地点速度方向与山坡所在的面向上方向成74°角.不计空气阻力,g=10m/s2,sin37°=0.6,则下列判断正确的是( )
如图所示,一架轰炸机在高度H=2155m的高空沿水平方向匀速飞行,在倾斜角度为θ=37°的山坡上方某一位置,先后自由释放两枚炸弹.其中先释放的炸弹正好垂直于斜面落在半山腰上的A点,后释放的炸弹正好落在山顶上的B点,落地点速度方向与山坡所在的面向上方向成74°角.不计空气阻力,g=10m/s2,sin37°=0.6,则下列判断正确的是( )| A. | 飞机飞行速度为150m/s | |
| B. | 山坡高为h=1500m | |
| C. | 两次投弹时间间隔7s | |
| D. | 飞机在两次投弹时相距的距离约为2007m |
 如图所示,+Q1和-Q2是两个可自由移动的电荷,且Q2=4Q1.现再取一个可自由移动的点电荷Q3放在Q1与Q2连接的直线上,欲使整个系统平衡,则Q3应为负电荷(填正或负),放在Q1的左边(填左或右).
如图所示,+Q1和-Q2是两个可自由移动的电荷,且Q2=4Q1.现再取一个可自由移动的点电荷Q3放在Q1与Q2连接的直线上,欲使整个系统平衡,则Q3应为负电荷(填正或负),放在Q1的左边(填左或右).

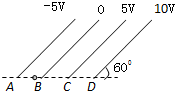 如图所示,为匀强电场中的一组等势面A、B、C、D,若 相邻两点间的距离都是2cm,则该电场的场强为$\frac{5\sqrt{3}}{3}×1{0}^{2}$V/m; 到A点距离为1.5cm的P点的电势为-1.25V; 该场强方向为垂直于等势面斜向上.
如图所示,为匀强电场中的一组等势面A、B、C、D,若 相邻两点间的距离都是2cm,则该电场的场强为$\frac{5\sqrt{3}}{3}×1{0}^{2}$V/m; 到A点距离为1.5cm的P点的电势为-1.25V; 该场强方向为垂直于等势面斜向上.