题目内容
3. 如图所示,一架轰炸机在高度H=2155m的高空沿水平方向匀速飞行,在倾斜角度为θ=37°的山坡上方某一位置,先后自由释放两枚炸弹.其中先释放的炸弹正好垂直于斜面落在半山腰上的A点,后释放的炸弹正好落在山顶上的B点,落地点速度方向与山坡所在的面向上方向成74°角.不计空气阻力,g=10m/s2,sin37°=0.6,则下列判断正确的是( )
如图所示,一架轰炸机在高度H=2155m的高空沿水平方向匀速飞行,在倾斜角度为θ=37°的山坡上方某一位置,先后自由释放两枚炸弹.其中先释放的炸弹正好垂直于斜面落在半山腰上的A点,后释放的炸弹正好落在山顶上的B点,落地点速度方向与山坡所在的面向上方向成74°角.不计空气阻力,g=10m/s2,sin37°=0.6,则下列判断正确的是( )| A. | 飞机飞行速度为150m/s | |
| B. | 山坡高为h=1500m | |
| C. | 两次投弹时间间隔7s | |
| D. | 飞机在两次投弹时相距的距离约为2007m |
分析 将A点和B点的速度进行分解,得出竖直分速度,结合下降的距离,根据竖直位移关系,联立方程组求出初速度和山坡的高度.根据落点的水平位移,结合几何关系求出两次投弹相距的距离,从而得出投弹的时间间隔.
解答 解:将A点的速度分解为水平方向和竖直方向,根据平行四边形定则知,vyA=v0cot37°,同理,B点的竖直分速度vyB=v0tan37°,
根据几何关系有:$H-\frac{{{v}_{0}}^{2}co{t}^{2}37°}{2g}=\frac{h}{2}$,$H-\frac{{{v}_{0}}^{2}ta{n}^{2}37°}{2g}=h$,
代入数据联立解得v0=120m/s,h=1750m,故A、B错误.
落在A点的水平位移${x}_{A}={v}_{0}•\frac{{v}_{0}cot37°}{g}=\frac{12{0}^{2}×\frac{4}{3}}{10}$m=1920m,落在B点的水平位移${x}_{B}={v}_{0}\frac{{v}_{0}tan37°}{g}=\frac{12{0}^{2}×\frac{3}{4}}{10}m$=1080m,
则两次投弹相距的距离△x=${x}_{A}+\frac{h}{2}cot37°-{x}_{B}$=$1920+\frac{1750}{2}×\frac{4}{3}-1080m$=2007m,则投弹的时间间隔$△t=\frac{△x}{{v}_{0}}=\frac{2007}{120}s=16.7s$,故C错误,D正确.
故选:D.
点评 本题考查了平抛运动规律的基本运用,知道平抛运动在水平方向和竖直方向上的运动规律,抓住速度限制,结合运动学公式灵活求解,本题对数学几何能力的要求较高,需加强这方面的训练.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 1.0×10-19C | B. | 1.8×10-19C | C. | 3.2×10-19C | D. | 4.5×10-19C |
| A. | 两质量均为m的铁球,球心相距为R时,两球之间的万有引力F=G$\frac{{m}^{2}}{{R}^{2}}$ | |
| B. | 静止在国际空间站内的宇航员的重力等于宇航员在该处所受地球的万有引力 | |
| C. | 静止在国际空间站内的宇航员从手中静止释放一物体,物体将竖直落向空间站地面 | |
| D. | 静止在国际空间站内的宇航员随空间站一起绕地球做圆周运动的向心力,等于地球对宇航员的万有引力和空间站对宇航员的支持力的合力 |
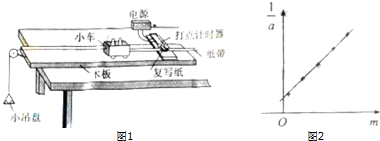
 测定木块与长木板之间的动摩擦因数时,采用如图1所示的装置,图中长木板水平固定.
测定木块与长木板之间的动摩擦因数时,采用如图1所示的装置,图中长木板水平固定.
 (量程3V,内阻RV=10kΩ)
(量程3V,内阻RV=10kΩ) (量程3mA,内阻RG=100Ω)
(量程3mA,内阻RG=100Ω)
 两个质点A和B同时由同一地点沿同一方向做直线运动,它们的速度-时间图象如图所示,则A做匀速直线运动,B做匀加速直线运动;它们的加速度aA=0m/s2,aB=5m/s2,当t=2秒时,它们的速度相同,此时它们各自的位移sA=40m,sB=20m;当它们再次相遇,此时离开出发地的位移为80m.
两个质点A和B同时由同一地点沿同一方向做直线运动,它们的速度-时间图象如图所示,则A做匀速直线运动,B做匀加速直线运动;它们的加速度aA=0m/s2,aB=5m/s2,当t=2秒时,它们的速度相同,此时它们各自的位移sA=40m,sB=20m;当它们再次相遇,此时离开出发地的位移为80m.