��Ŀ����
13����ͼ����ʾ�������ѹ��ԭ������Ȧ��������n1��n2=4��1��ԭ��Ȧ��ͼ����ʾ�����ҽ����磬����Ȧ�������ѹ�����������������������RT����ֵ���¶ȵ����߶���С����������P�������裩��ɱպϵ�·����·�е������ӵ�һ��ֵʱ������P���������������������ж���ȷ���ǣ�������
| A�� | ��ѹ��ԭ��Ȧ�н�����ѹ��˲ʱ����ʽu=36sin��100��t�� V | |
| B�� | ��ѹ��ʾ��Ϊ9 V | |
| C�� | RT���¶����ߵ�һ��ֵʱ��������P���ᷢ�������� | |
| D�� | RT���¶�����ʱ����ѹ�������빦�ʱ�С |
���� ��ͼ�ҿ�֪������ѹ���ֵUm=36$\sqrt{2}$V������T=0.02s����������������ٶȵ�ֵ����ɵý�����ѹu�ı���ʽ u=Umsin��t��V�����ɱ�ѹ��ԭ���ɵñ�ѹ��ԭ������Ȧ�еĵ���֮�ȣ����롢�������֮�ȣ�Rt���¶�����ʱ����ֵ��С�����ݸ��ص���ı仯����֪��������ѹ�仯��
��� �⣺A��ԭ��Ȧ�ӵ�ͼ����ʾ�����ҽ����磬��ͼ֪����ѹ36$\sqrt{2}$V������0.02S���ʽ��ٶ��Ǧ�=100�У�u=36$\sqrt{2}$sin100��t��V������A����
B�������ѹ��ԭ������Ȧ��������n1��n2=4��1�����Ը���Ȧ�ĵ�ѹ��U2=9V��
���Ե�ѹ��ʾ��С��9V����B����
C��Rt���¶�����ʱ����Ȧ�е����������ߵ�һ��ֵʱ��������P���ᷢ������������C��ȷ��
D��Rt���¶�����ʱ����Ȧ�е�����������Ȧ�ĵ�ѹ���䣬��ѹ����������ʱ�������ѹ�������롢�������֮��Ϊ1��1����ѹ�������빦�ʱ��D����
��ѡ��C��
���� ����ͼ��ȷ�ҳ���֪�����Ƕ�ѧ����ͼ�Ļ���Ҫ��ȷ���������ѹ�����ص㼰��ѹ���������������ȵĹ�ϵ���ǽ������Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
3�� Ϊ��ʹ�˿ͳ˳���Ϊ���ʣ������꼶ij�����С�����һ���µ����Σ������ο�������·���¶ȵı仯���Զ�������ʹ�������ϱ���ʼ�ձ���ˮƽ����ͼ��ʾ�����˳���������ʱ��һλ�˿����������������ϣ�������˵����ȷ���ǣ�������
Ϊ��ʹ�˿ͳ˳���Ϊ���ʣ������꼶ij�����С�����һ���µ����Σ������ο�������·���¶ȵı仯���Զ�������ʹ�������ϱ���ʼ�ձ���ˮƽ����ͼ��ʾ�����˳���������ʱ��һλ�˿����������������ϣ�������˵����ȷ���ǣ�������
 Ϊ��ʹ�˿ͳ˳���Ϊ���ʣ������꼶ij�����С�����һ���µ����Σ������ο�������·���¶ȵı仯���Զ�������ʹ�������ϱ���ʼ�ձ���ˮƽ����ͼ��ʾ�����˳���������ʱ��һλ�˿����������������ϣ�������˵����ȷ���ǣ�������
Ϊ��ʹ�˿ͳ˳���Ϊ���ʣ������꼶ij�����С�����һ���µ����Σ������ο�������·���¶ȵı仯���Զ�������ʹ�������ϱ���ʼ�ձ���ˮƽ����ͼ��ʾ�����˳���������ʱ��һλ�˿����������������ϣ�������˵����ȷ���ǣ�������| A�� | �˿����ܵ��ĺ�����������ֱ���� | |
| B�� | ֧�������ܴ������� | |
| C�� | ���˿�δ�Ӵ����ο�������Ӧ�ܵ���ǰ��ˮƽ����Ħ�������� | |
| D�� | �˿ʹ��ڳ���״̬ |
4��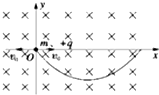 һ��Բ��һֱ�������ع�������Բ��һ�̶����������Ĺ켣��Ϊ���ߣ�����ֱƽ������xOy����ϵ���ռ���ڴ�ֱxOyƽ���������ǿ�ų����Ÿ�Ӧǿ��ΪB��һ����Ϊm�������Ϊ+q��С�������ԭ���ɾ�ֹ�ͷţ�С��Ĺ켣���ǰ��ߣ�С����O���ٶ�Ϊ0ʱ�����Էֽ�Ϊ��Сʼ����ȵ�һˮƽ���Һ�һˮƽ������������ٶȣ�����ٶȴ�Сȡ�ʵ���ֵ���Ϳ���С����˶��ֽ����v0���ٶ�����������ֱ���˶��ʹ�O����v1Ϊ���ٶ�������Բ���˶��������˶������������ٶ�Ϊg������ʽ����ȷ���ǣ�������
һ��Բ��һֱ�������ع�������Բ��һ�̶����������Ĺ켣��Ϊ���ߣ�����ֱƽ������xOy����ϵ���ռ���ڴ�ֱxOyƽ���������ǿ�ų����Ÿ�Ӧǿ��ΪB��һ����Ϊm�������Ϊ+q��С�������ԭ���ɾ�ֹ�ͷţ�С��Ĺ켣���ǰ��ߣ�С����O���ٶ�Ϊ0ʱ�����Էֽ�Ϊ��Сʼ����ȵ�һˮƽ���Һ�һˮƽ������������ٶȣ�����ٶȴ�Сȡ�ʵ���ֵ���Ϳ���С����˶��ֽ����v0���ٶ�����������ֱ���˶��ʹ�O����v1Ϊ���ٶ�������Բ���˶��������˶������������ٶ�Ϊg������ʽ����ȷ���ǣ�������
 һ��Բ��һֱ�������ع�������Բ��һ�̶����������Ĺ켣��Ϊ���ߣ�����ֱƽ������xOy����ϵ���ռ���ڴ�ֱxOyƽ���������ǿ�ų����Ÿ�Ӧǿ��ΪB��һ����Ϊm�������Ϊ+q��С�������ԭ���ɾ�ֹ�ͷţ�С��Ĺ켣���ǰ��ߣ�С����O���ٶ�Ϊ0ʱ�����Էֽ�Ϊ��Сʼ����ȵ�һˮƽ���Һ�һˮƽ������������ٶȣ�����ٶȴ�Сȡ�ʵ���ֵ���Ϳ���С����˶��ֽ����v0���ٶ�����������ֱ���˶��ʹ�O����v1Ϊ���ٶ�������Բ���˶��������˶������������ٶ�Ϊg������ʽ����ȷ���ǣ�������
һ��Բ��һֱ�������ع�������Բ��һ�̶����������Ĺ켣��Ϊ���ߣ�����ֱƽ������xOy����ϵ���ռ���ڴ�ֱxOyƽ���������ǿ�ų����Ÿ�Ӧǿ��ΪB��һ����Ϊm�������Ϊ+q��С�������ԭ���ɾ�ֹ�ͷţ�С��Ĺ켣���ǰ��ߣ�С����O���ٶ�Ϊ0ʱ�����Էֽ�Ϊ��Сʼ����ȵ�һˮƽ���Һ�һˮƽ������������ٶȣ�����ٶȴ�Сȡ�ʵ���ֵ���Ϳ���С����˶��ֽ����v0���ٶ�����������ֱ���˶��ʹ�O����v1Ϊ���ٶ�������Բ���˶��������˶������������ٶ�Ϊg������ʽ����ȷ���ǣ�������| A�� | �ٶ�v0��ȡ���ʵ�ֵӦΪ$\frac{mg}{2qB}$ | |
| B�� | ����t=$\frac{2��m}{qB}$��һ�ε��������͵� | |
| C�� | ��͵��y������Ϊy=$\frac{-{m}^{2}g}{{q}^{2}{B}^{2}}$ | |
| D�� | ��͵���ٶ�Ϊ2v0 |
1�� ��ͼ��ʾ����б�涥��a�����ٶ�vaˮƽ�׳�һС����ʱ��taǡ������б���P��������P�����Ϸ���a�ȸߵ�b�����ٶ�vbˮƽ�׳���һС����ʱ��tbǡ������б����е�O���������ƿ������������й�ϵʽ��ȷ�ģ�������
��ͼ��ʾ����б�涥��a�����ٶ�vaˮƽ�׳�һС����ʱ��taǡ������б���P��������P�����Ϸ���a�ȸߵ�b�����ٶ�vbˮƽ�׳���һС����ʱ��tbǡ������б����е�O���������ƿ������������й�ϵʽ��ȷ�ģ�������
 ��ͼ��ʾ����б�涥��a�����ٶ�vaˮƽ�׳�һС����ʱ��taǡ������б���P��������P�����Ϸ���a�ȸߵ�b�����ٶ�vbˮƽ�׳���һС����ʱ��tbǡ������б����е�O���������ƿ������������й�ϵʽ��ȷ�ģ�������
��ͼ��ʾ����б�涥��a�����ٶ�vaˮƽ�׳�һС����ʱ��taǡ������б���P��������P�����Ϸ���a�ȸߵ�b�����ٶ�vbˮƽ�׳���һС����ʱ��tbǡ������б����е�O���������ƿ������������й�ϵʽ��ȷ�ģ�������| A�� | va=vb | B�� | va=$\sqrt{2}$vb | C�� | ta=$\sqrt{2}$tb | D�� | ta=2tb |
18�� 2014��3��8���賿�����ͻ�ʧ�����������Dz�����Ľ������������ơ��߷֡�ң��4���ͺŽ�10�����ǣ�Ϊ�����Ѿ��ṩ����֧�֣��ر��ǡ��߷�һ�š�ͻ���˿ռ�ֱ��ʡ���������������ϵĴ����ؼ���������ͼΪ���߷�һ�š��뱱������ϵͳ���������ڿ���ijһ�����˶���ʾ��ͼ����������ϵͳ���������ǡ�G1���͡�G3���Լ����߷�һ�š�������Ϊ�Ƶ���O������Բ���˶������ǡ�G1���͡�G3���Ĺ���뾶Ϊr��ijʱ�����Ź������Ƿֱ�λ�ڹ���ϵ�A��B��λ�ã����߷�һ�š���Cλ�ã������Ǿ�˳ʱ�����У�������洦���������ٶ�Ϊg������뾶ΪR���������Ǽ�����������������˵����ȷ���ǣ�������
2014��3��8���賿�����ͻ�ʧ�����������Dz�����Ľ������������ơ��߷֡�ң��4���ͺŽ�10�����ǣ�Ϊ�����Ѿ��ṩ����֧�֣��ر��ǡ��߷�һ�š�ͻ���˿ռ�ֱ��ʡ���������������ϵĴ����ؼ���������ͼΪ���߷�һ�š��뱱������ϵͳ���������ڿ���ijһ�����˶���ʾ��ͼ����������ϵͳ���������ǡ�G1���͡�G3���Լ����߷�һ�š�������Ϊ�Ƶ���O������Բ���˶������ǡ�G1���͡�G3���Ĺ���뾶Ϊr��ijʱ�����Ź������Ƿֱ�λ�ڹ���ϵ�A��B��λ�ã����߷�һ�š���Cλ�ã������Ǿ�˳ʱ�����У�������洦���������ٶ�Ϊg������뾶ΪR���������Ǽ�����������������˵����ȷ���ǣ�������
 2014��3��8���賿�����ͻ�ʧ�����������Dz�����Ľ������������ơ��߷֡�ң��4���ͺŽ�10�����ǣ�Ϊ�����Ѿ��ṩ����֧�֣��ر��ǡ��߷�һ�š�ͻ���˿ռ�ֱ��ʡ���������������ϵĴ����ؼ���������ͼΪ���߷�һ�š��뱱������ϵͳ���������ڿ���ijһ�����˶���ʾ��ͼ����������ϵͳ���������ǡ�G1���͡�G3���Լ����߷�һ�š�������Ϊ�Ƶ���O������Բ���˶������ǡ�G1���͡�G3���Ĺ���뾶Ϊr��ijʱ�����Ź������Ƿֱ�λ�ڹ���ϵ�A��B��λ�ã����߷�һ�š���Cλ�ã������Ǿ�˳ʱ�����У�������洦���������ٶ�Ϊg������뾶ΪR���������Ǽ�����������������˵����ȷ���ǣ�������
2014��3��8���賿�����ͻ�ʧ�����������Dz�����Ľ������������ơ��߷֡�ң��4���ͺŽ�10�����ǣ�Ϊ�����Ѿ��ṩ����֧�֣��ر��ǡ��߷�һ�š�ͻ���˿ռ�ֱ��ʡ���������������ϵĴ����ؼ���������ͼΪ���߷�һ�š��뱱������ϵͳ���������ڿ���ijһ�����˶���ʾ��ͼ����������ϵͳ���������ǡ�G1���͡�G3���Լ����߷�һ�š�������Ϊ�Ƶ���O������Բ���˶������ǡ�G1���͡�G3���Ĺ���뾶Ϊr��ijʱ�����Ź������Ƿֱ�λ�ڹ���ϵ�A��B��λ�ã����߷�һ�š���Cλ�ã������Ǿ�˳ʱ�����У�������洦���������ٶ�Ϊg������뾶ΪR���������Ǽ�����������������˵����ȷ���ǣ�������| A�� | ���ǡ�G1���͡�G3���ļ��ٶȴ�С�����Ϊ$\frac{{R}^{2}}{{r}^{2}}g$ | |
| B�� | ����������߷�һ�š����ǿ��ٵ���Bλ�õ��·������������� | |
| C�� | ���ǡ�G1����λ��A�˶���λ��B�����ʱ��Ϊ$\frac{2��}{3R}\sqrt{\frac{r}{g}}$ | |
| D�� | �����߷�һ�š����ڸ߶ȴ���ϡ�����壬������һ��ʱ���е�ܻ����� |
5����ֹ�ڴֲ�ˮƽ���ϵ����壬��ˮƽ����F��������ֱ���˶�����v-tͼ����ͼ��ʾ��������


| A�� | ��0-t1ʱ���ڣ�����F��Сһ���������� | |
| B�� | ��t1ʱ�̣�����FΪ�� | |
| C�� | ��t1-t2ʱ���ڣ�����F��С���ܲ��ϼ�С | |
| D�� | ��t1-t2ʱ���ڣ�������������Ϊ�� |
 ��ͼ��ʾ���뾶ΪR�ľ�Ե�⻬Բ���̶�����ֱƽ���ڣ�������һ����Ϊm�Ҵ�����ɵ����ӣ��ռ����ˮƽ���ҵ���ǿ�糡���������ܾ���������������$\frac{3}{4}$���������Ӵӻ������λ��A�㾲ֹ�ͷţ�
��ͼ��ʾ���뾶ΪR�ľ�Ե�⻬Բ���̶�����ֱƽ���ڣ�������һ����Ϊm�Ҵ�����ɵ����ӣ��ռ����ˮƽ���ҵ���ǿ�糡���������ܾ���������������$\frac{3}{4}$���������Ӵӻ������λ��A�㾲ֹ�ͷţ� ��ͼ��ʾ������ֱƽ���ڣ��������Ϊ�⻬�����Բ�ι���İ뾶ΪR������Ϊm��С����б���Ͼ�ˮƽ���h=2.5R��A���ɾ�ֹ��ʼ�»������ͨ��������Ӵ���B��C��ʱ����е����ʧ����
��ͼ��ʾ������ֱƽ���ڣ��������Ϊ�⻬�����Բ�ι���İ뾶ΪR������Ϊm��С����б���Ͼ�ˮƽ���h=2.5R��A���ɾ�ֹ��ʼ�»������ͨ��������Ӵ���B��C��ʱ����е����ʧ���� ��ͼ��ʾ������Ϊm��С����ϸ���������컨���ϣ�������ֱƽ���ڸ�С���һ��С���䡢����ɸı����F=$\frac{1}{2}$mg����ʹС�����±���ƽ�⣬��ϸ������ֱ����ļн����Ϊ��������
��ͼ��ʾ������Ϊm��С����ϸ���������컨���ϣ�������ֱƽ���ڸ�С���һ��С���䡢����ɸı����F=$\frac{1}{2}$mg����ʹС�����±���ƽ�⣬��ϸ������ֱ����ļн����Ϊ��������