题目内容
20．质量为M的火箭以速度v0飞行在太空中，现在突然向后喷出一份质量为△m的气体，喷出的气体相对于火箭的速度是v，喷气后火箭的速度是多少？分析 以火箭和喷出的气体为研究对象，应用动量守恒定律，可以求出喷气后火箭的速度
解答 解：以火箭和喷出的气体为研究对象，以火箭飞行的方向为正方向，由动量守恒定律得：
Mv0=（M-△m）v′+△m（v′-v），
解得：v′=v0+$\frac{△m}{M}$v；
答：喷气后火箭的速度是v0+$\frac{△m}{M}$v．
点评 本题考查了求火箭的速度，应用动量守恒定律即可正确解题，解题时要注意研究对象的选择、正方向的选取．
练习册系列答案
阅读快车系列答案
相关题目
16．
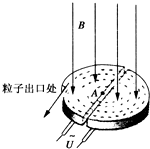劳伦斯和利文斯设计出回旋加速器．置于高真空中的D形金属盒半径为R，两盒间的狭缝很小，带电粒子穿过的时间可忽略．磁感应强度为B的匀强磁场与盒面垂直，高频交流电频率为f，加速电压为U．若A处粒子源产生的质子质量为m、电荷量为+q，在加速器中被加速，且加速过程中不考虑相对论效应和重力的影响．则下列说法正确的是（ ）
劳伦斯和利文斯设计出回旋加速器．置于高真空中的D形金属盒半径为R，两盒间的狭缝很小，带电粒子穿过的时间可忽略．磁感应强度为B的匀强磁场与盒面垂直，高频交流电频率为f，加速电压为U．若A处粒子源产生的质子质量为m、电荷量为+q，在加速器中被加速，且加速过程中不考虑相对论效应和重力的影响．则下列说法正确的是（ ）| A． | 质子被加速后的最大速度不可能超过2πRf | |
| B． | 质子离开回旋加速器时的最大动能与加速电压U成正比 | |
| C． | 质子第2次和第1次经过两D形盒间狭缝后轨道半径之比为$\sqrt{2}$：1 | |
| D． | 不改变磁感应强度B和交流电频率f，也能用于加速α粒子 |
11．如图电路中，当滑动变阻器的触头P向上滑动时，则（ ）
| A． | 电源的总功率变小 | B． | 电容器贮存的电量变大 | ||
| C． | 灯L1变亮 | D． | 灯L2变暗 |
如图所示，物重30N，用AC绳悬挂在A点，再用一绳系在AC绳的中点O，现用水平力缓慢地拉OB，当OA绳拉到与竖直方向成30°角时，绳OA和OB的拉力分别是多大？
12．
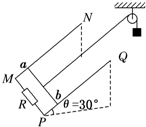如图所示，足够长的光滑平行导轨MN、PQ倾斜放置，两导轨间距离为L=1.0m，导轨平面与水平面间的夹角为30°，磁感应强度为B的匀强磁场垂直于导轨平面向上，导轨的M、P两端连接阻值为R=3.0Ω的电阻，金属棒ab垂直于导轨放置并用细线通过光滑定滑轮与重物相连，金属棒ab的质量m=0.20kg，电阻r=0.50Ω，重物的质量M=0.60kg，如果将金属棒和重物由静止释放，金属棒沿斜面上滑的距离与时间的关系如表所示，不计导轨电阻，g取10m/s2．求：
（1）ab棒最终做匀速直线运动的速度是多少？
（2）磁感应强度B的大小是多少？
（3）当金属棒ab的速度v=0.7m/s时，金属棒ab上滑的加速度大小是多少？
如图所示，足够长的光滑平行导轨MN、PQ倾斜放置，两导轨间距离为L=1.0m，导轨平面与水平面间的夹角为30°，磁感应强度为B的匀强磁场垂直于导轨平面向上，导轨的M、P两端连接阻值为R=3.0Ω的电阻，金属棒ab垂直于导轨放置并用细线通过光滑定滑轮与重物相连，金属棒ab的质量m=0.20kg，电阻r=0.50Ω，重物的质量M=0.60kg，如果将金属棒和重物由静止释放，金属棒沿斜面上滑的距离与时间的关系如表所示，不计导轨电阻，g取10m/s2．求：| 时间t（s） | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
| 上滑距离（m） | 0 | 0.05 | 0.15 | 0.35 | 0.70 | 1.05 | 1.40 |
（2）磁感应强度B的大小是多少？
（3）当金属棒ab的速度v=0.7m/s时，金属棒ab上滑的加速度大小是多少？
9．
如图所示，将两个质量分别为m、3m的小球a、b用细线相连悬挂于O点，用力F拉小球a，使整个装置处于平衡状态，且悬线Oa与竖直方向成30°角，则力F的大小（ ）
如图所示，将两个质量分别为m、3m的小球a、b用细线相连悬挂于O点，用力F拉小球a，使整个装置处于平衡状态，且悬线Oa与竖直方向成30°角，则力F的大小（ ）| A． | 可能为$\sqrt{3}$mg | B． | 可能为$\frac{\sqrt{3}}{2}$mg | C． | 可能为2mg | D． | 可能为3mg |