题目内容
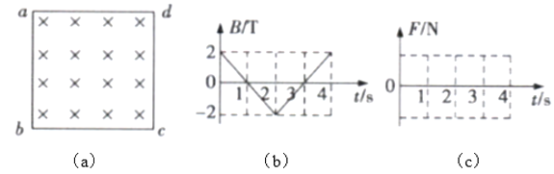
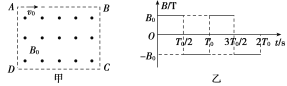
【题目】如图甲所示,比荷![]() =k的带正电的粒子(可视为质点),以速度v0从A点沿AB方向射入长方形磁场区域,长方形的长AB=
=k的带正电的粒子(可视为质点),以速度v0从A点沿AB方向射入长方形磁场区域,长方形的长AB=![]() L,宽AD=L。取粒子刚进入长方形区域的时刻为0时刻,垂直于长方形平面的磁感应强度按图乙所示规律变化(以垂直纸面向外的磁场方向为正方向),粒子仅在洛伦兹力的作用下运动。
L,宽AD=L。取粒子刚进入长方形区域的时刻为0时刻,垂直于长方形平面的磁感应强度按图乙所示规律变化(以垂直纸面向外的磁场方向为正方向),粒子仅在洛伦兹力的作用下运动。
(1)若带电粒子在通过A点后的运动过程中不再越过AD边,要使其恰能沿DC方向通过C点,求磁感应强度B0及其磁场的变化周期T0为多少?
(2)要使带电粒子通过A点后的运动过程中不再越过AD边,求交变磁场磁感应强度B0和变化周期T0的乘积B0T0应满足什么关系?
【答案】(1)![]() (n=1,2,3…),T0=
(n=1,2,3…),T0=![]() (n=1,2,3…),(2)B0T0≤
(n=1,2,3…),(2)B0T0≤![]() 。
。
【解析】
(1)带电粒子在长方形区域内做匀速圆周运动,设粒子运动轨迹半径为R,周期为T,则可得
![]()
解得:R=![]() =
=![]()
周期:
T![]() =
=![]()
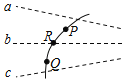
每经过一个磁场的变化周期,粒子的末速度方向和初速度方向相同,如图所示,
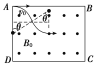
要使粒子恰能沿DC方向通过C点,则经历的时间必须是磁场周期的整数倍,AB方向:
![]() L=n·2Rsinθ
L=n·2Rsinθ
BC方向:
L=n·2R(1-cosθ)
解得:cosθ=1(舍去),cosθ=![]()
所以θ=60°,又:
R=![]()
即:
B0=![]() (n=1、2、3…)
(n=1、2、3…)
T0=![]() (n=1、2、3…);
(n=1、2、3…);
(2) 当交变磁场周期取最大值而粒子不再越过AD边时运动情形如图所示
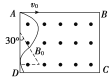
由图可知粒子在第一个![]() T0时间内转过的圆心角:
T0时间内转过的圆心角:
θ=![]()
则:
T0≤![]() T
T
即T0≤![]() ·
·![]() ≤
≤![]()
所以:
B0T0≤![]() 。
。

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目